【题目】如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线![]() 过点A(—1,0),与⊙C相切于点D,
过点A(—1,0),与⊙C相切于点D,
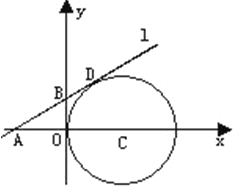
(1)求∠CAD的度数。
(2)求直线![]() 的解析式。
的解析式。
参考答案:
【答案】(1)30°(2)y=![]() x+
x+![]()
【解析】
试题分析:(1)连接CD,由于直线l为⊙C的切线,故CD⊥AD.C点坐标为(1,0),故OC=1,即⊙C的半径为1,由点A的坐标为(-1,0),可求出∠CAD=30度.作DE⊥AC于E点,则∠CDE=∠CAD=30°;(2)可求出CE=![]() ,点B的坐标为(0,
,点B的坐标为(0, ![]() ).设直线l的函数解析式为y=kx+b,把A,B两点的坐标代入即可求出未知数的值从而求出其解析式.
).设直线l的函数解析式为y=kx+b,把A,B两点的坐标代入即可求出未知数的值从而求出其解析式.
试题解析:(1)连接CD,∵直线![]() 为⊙C的切线,∴CD⊥AD。∵C点坐标为(1,0),∴OC=1,即⊙C的半径为1,∴CD=OC=1。
为⊙C的切线,∴CD⊥AD。∵C点坐标为(1,0),∴OC=1,即⊙C的半径为1,∴CD=OC=1。
又∵点A的坐标为(-1,0),∴AC=2,∴∠CAD=30°。
(2)作DE⊥AC于E点,则∠CDE=∠CAD=30°,∴CE=![]() ,
,
![]() ,∴OE=OC-CE=
,∴OE=OC-CE=![]() ,∴点D的坐标为(
,∴点D的坐标为(![]() ,
,![]() )。
)。
设直线![]() 的函数解析式为
的函数解析式为![]() ,则
,则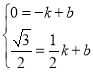
解得k=![]() ,b=
,b=![]() ,
,
∴直线![]() 的函数解析式为y=
的函数解析式为y=![]() x+
x+![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A. 任何数的零次幂都等于1
B. 对角线相等且垂直的四边形是正方形
C. 有一条边相等的两个等腰直角三角形全等
D. 有两条直角边对应相等的两个直角三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(a+b)2-2(a+b)-3=0,则a+b=_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙M与x轴相切于原点,平行于y轴的直线交圆于P、Q两点,P点在Q点的下方,若P点的坐标是(2,1),则圆心M的坐标是( )

A.(0,3) B.(0,2.5) C.(0,2) D.(0,1.5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
 的图象交于A(-2,1),B(1,n)两点.
的图象交于A(-2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC.抛物线y=ax2+bx+c经过点A、B、C.
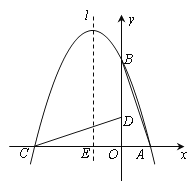
(1)求抛物线的解析式.
(2)若点P是第二象限内抛物线上的动点,其横坐标为t.
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时点P的坐标.
 ②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由.
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD面积的最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.

(1)求抛物线的解析式;
 (2)求△MCB的面积S△MCB.
(2)求△MCB的面积S△MCB.
相关试题

