搜索
【题目】如图，在平面直角坐标系中，已知l1∥l2，直线l1经过原点O，直线l2对应的函数表达式为
，点A在直线l2上，AB⊥l1，垂足为B，则线段AB的长为（ ）
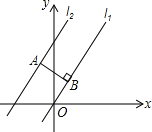
A. 4 B. 6 C. 8 D. 
参考答案：
【答案】D
【解析】
过点O作OC垂直于l2交点为C,得出四边形OCAB是矩形,则OC=AB;分别求得l2与两个坐标轴的交点坐标,在l2与两个坐标轴围成的直角三角形中利用勾股定理与三角形的面积求得OC即可得出答案
解:如图,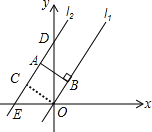
过点O作OC垂直于l2交点为C
∵l1∥l2, AB⊥l1, OC⊥l2
∴四边形OCAB是矩形,
∴OC=AB
∵直线l2与两个坐标轴的交点坐标分别为D(0,8),E(-6,0)
∴DE=
=10
∴
DE×OC=OE×OD
即×10×OC=×6×8
解得:OC=
∴AB=
故选D
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列四个图形中，是轴对称图形的是（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠1=∠2，那么添加一个条件后，仍无法判定△ABD≌△ACD的是（ ）
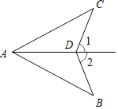
A. AB=AC B. ∠B=∠C C. AD平分∠CAB D. CD=BD
-
科目： 来源： 题型：
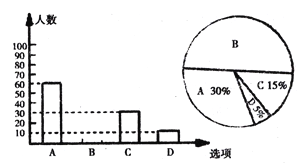
查看答案和解析>>【题目】为了解学生参加体育活动的情况，学校对学生进行随机抽样调查，其中一个问题是“你平均每天参加体育活动的时间是多少？”共有4个选题．
A．1.5小时以上 B．1～1.5小时 C．0.5～1小时 D．0.5小时以下
请你根据统计图提供的信息，解答以下问题：
（1）本次一共调查了多少名学生？
（2）将条形统计图选项B补充完整；
（3）若该校有3000名学生，你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下？
-
科目： 来源： 题型：
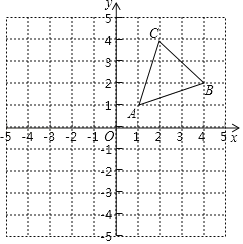
查看答案和解析>>【题目】已知，在如图所示的网格中建立平面直角坐标系后，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（2，4）．
（1）画出△ABC关于y轴对称的△A1B1C1；
（2）①借助图中的网格，请只用直尺（不含刻度）在图中找一点P，使得P到AB、AC的距离相等，且PA=PB．
②若x轴上有一动点Q，使得△QAB的周长最小，则△QAB的最小周长为 ．
（友情提醒：请别忘了标注宇母）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=AC，点D为直线BC上一动点（点D不与B、C重合）以AD为边作正方形ADEF，使∠DAF=∠BAC，连接CF．
（1）如图1，当点D在线段BC上时，求证：BD=CF；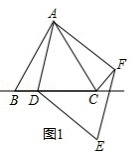
（2）如图2，当点D在线段BC的延长线上，且∠BAC=90°时．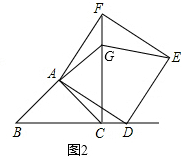
①问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；
②延长BA交CF于点G，连接GE，若AB=2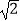
，CD=BC，请求出GE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB、AC边的垂直平分线分别交BC边于点M、N．
(1)如图①，若△AMN是等边三角形，则∠BAC= °；
(2)如图②，若∠BAC=135°，求证：BM2+CN2=MN2．
(3)如图③，∠ABC的平分线BP和AC边的垂直平分线相交于点P，过点P作PH垂直BA的延长线于点H．若AB=4，CB=10，求AH的长．
相关试题
