【题目】完成下面推理过程
如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
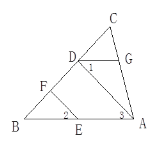
解: 因为EF∥AD,
所以∠2=____ (_________________________________)
又因为∠1=∠2
所以∠1=∠3 (__________________)
所以AB∥_____ (___________________________________)
所以∠BAC+______=180°(___________________________)
因为∠BAC=70°
所以∠AGD=_______.
参考答案:
【答案】见解析
【解析】
根据平行线的性质推出∠1=∠2=∠3,推出AB∥DG,根据平行线的性质得出∠BAC+∠AGD=180°,代入求出即可.
因为EF∥AD
所以∠2=__∠3__ (_两直线平行,同位角相等_)
又因为∠1=∠2
所以∠1=∠3 (___等量代换_)
所以AB∥_DG_ (__内错角相等,两直线平行_)
所以∠BAC+__∠AGD _=180°(_两直线平行,同旁内角相等_)
因为∠BAC=70°
所以∠AGD=_110°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中有3张形状大小完全相同的卡片,编号为1,2,3,先任取一张,将其编号记为m,再从剩下的两张中任取一张,将其编号记为n.
(1)请用树状图或者列表法,表示事件发生的所有可能情况;
(2)求关于x的方程x2+mx+n=0有两个不相等实数根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点(0.5,0),有下列结论:
①abc>0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c>0;⑤a﹣b≥m(am﹣b).
其中所有正确的结论是( )
A.①②③
B.①③④
C.①②③⑤
D.①③⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画
 ,连结AF,CF,则图中阴影部分面积为 .
,连结AF,CF,则图中阴影部分面积为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】去年某省将地处A、B两地的两所大学合并成了一所综合性大学,为了方便A、B两地师生的交往,学校准备在相距2km的A、B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向、B地的西偏北45°方向C处有一个半径为0.7km的公园,问计划修筑的这条公路会不会穿过公园?为什么?(
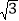 ≈1.732)
≈1.732)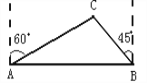
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
 中,
中, 为直线
为直线 上一点,
上一点, 为直线
为直线 上一点,
上一点,


(1)如图1,当
 在
在 上,
上, 在
在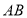 上时,求证
上时,求证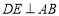 ;
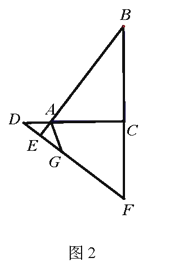
;(2)如图2,当
 在
在 的延长线上,
的延长线上, 在
在 的延长线上时,点
的延长线上时,点 在
在 上,连接
上,连接 ,且
,且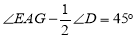 ,求证:
,求证:
(3)如图3,在(2)的条件下,连接
 当
当 平分
平分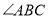 时,将
时,将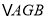 沿着
沿着 折至
折至 探究
探究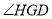 与
与 的数量关系.
的数量关系.
相关试题

