搜索
【题目】如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC，则AM平分∠DAB吗？试说明理由。（提示：过点M作ME垂直AD于E）。
参考答案：
【答案】见解析
【解析】试题分析：过M作ME⊥AD，根据DM平分∠ADC得到∠1=∠2，根据角平分线的性质得出ME=MC，根据中点得出MC=MB，则ME=MB，然后根据角平分线的逆定理得出答案．
试题解析：AM平分∠DAB
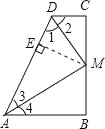
理由：过点M作ME⊥AD，垂足为E， ∵DM平分∠ADC， ∴∠1=∠2，
∵MC⊥CD，ME⊥AD， ∴ME=MC（角平分线上的点到角两边的距离相等），
又∵MC=MB， ∴ME=MB，
∵MB⊥AB，ME⊥AD，∴AM平分∠DAB（到角的两边距离相等的点在这个角的平分线上）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读材料
小明遇到这样一个问题：求计算
所得多项式的一次项系数．小明想通过计算
所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法．他决定从简单情况开始，先找
所得多项式中的一次项系数．通过观察发现：
也就是说，只需用
中的一次项系数1乘以
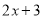中的常数项3，再用
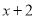中的常数项2乘以
中的一次项系数2，两个积相加
，即可得到一次项系数．延续上面的方法，求计算
所得多项式的一次项系数．可以先用
的一次项系数1， 
的常数项3， 
的常数项4，相乘得到12；再用
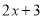的一次项系数2， 
的常数项2， 
的常数项4，相乘得到16；然后用
的一次项系数3， 
的常数项2， 
的常数项3，相乘得到18．最后将12，16，18相加，得到的一次项系数为46．参考小明思考问题的方法，解决下列问题：
（1）计算
所得多项式的一次项系数为 ．（2）计算
所得多项式的一次项系数为 ．（3）若计算
所得多项式的一次项系数为0，则
=_________．（4）若
是
的一个因式，则
的值为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
对于平面图形A，如果存在一个圆，使图形A上的任意一点到圆心的距离都不大于这个圆的半径，则称图形A被这个圆所覆盖.
对于平面图形A，如果存在两个或两个以上的圆，使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径，则称图形A被这些圆所覆盖.
例如：图1中①的三角形被一个圆覆盖，②中的四边形被两个圆所覆盖.
回答下列问题：
(1)边长为1 cm的正方形被一个半径为r的圆所覆盖，r的最小值是______ cm;
(2)边长为1 cm的等边三角形被一个半径为r的圆所覆盖，r的最小值是_____ cm;
(3)长为2 cm，宽为1 cm的矩形被两个半径均为r的圆所覆盖，r的最小值是_____ cm.这两个圆的圆心距是_____ cm.。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB、CD被直线EF所截，∠1=50°，下列说法错误的是（ ）
A．如果∠5=50°，那么AB∥CD B．如果∠4=130°，那么AB∥CD
C．如果∠3=130°，那么AB∥CD D．如果∠2=50°，那么AB∥CD
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A（﹣2，4），B（﹣2，1），C（﹣5，2）．
（1）请画出△ABC关于x轴对称的△A1B1C1．
（2）将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以﹣2，得到对应的点A2，B2，C2，请画出△A2B2C2．
（3）求△A1B1C1与△A2B2C2的面积比．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次物理竞赛中,有一道四选二的双项选择题,评分标准是:多选或只要选错一项就不得分,只选一项且对得1分,全对得3分.
(1)小娟在不会做的情况下,根据题意决定任选一项作为答案,求她得到1分的概率.
(2)小娜在不会做的情况下,根据题意决定任选两项作答案,用列表法表示小娜答案的所有可能结果,并求她得到3分的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：△ABC在坐标平面内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）.（正方形网格中， 每个小正方形的边长是1个单位长度）
（1）画出△ABC向下平移4个单位得到的△A1B1C1，并直接写出C1点的坐标；
（2）以点B为位似中心，在网格中画出△A2BC2，使△A2BC2与△ABC位似，且位似比为2︰1，并直接写出C2点的坐标及△A2BC2的面积．
相关试题
