搜索
【题目】已知：△ABC在坐标平面内，三个顶点的坐标分别为A（0，3），B（3，4），C（2，2）.（正方形网格中， 每个小正方形的边长是1个单位长度）
（1）画出△ABC向下平移4个单位得到的△A1B1C1，并直接写出C1点的坐标；
（2）以点B为位似中心，在网格中画出△A2BC2，使△A2BC2与△ABC位似，且位似比为2︰1，并直接写出C2点的坐标及△A2BC2的面积．
参考答案：
【答案】（1）画图见解析，C1(2，－2)；（2）画图见解析，C2（1,0） △A2BC2的面积等于10
【解析】分析：（1）根据网格结构，找出点A、B、C向下平移4个单位的对应点
、
、
的位置，然后顺次连接即可，再根据平面直角坐标系写出点的坐标；（2）延长BA到
使A=AB，延长BC到
，使C=BC，然后连接A2C2即可，再根据平面直角坐标系写出点的坐标，利用△B所在的矩形的面积减去四周三个小直角三角形的面积，列式计算即可得解．
本题解析：（1）如图，△A1B1C1即为所求，C1(2，－2)
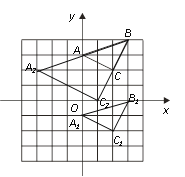
(2)如图,△B为所求, (1,0)，
△B 的面积：
6×4
×2×6×2×4×2×4=24644=2414=10，
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠B=∠C=90°，M是BC的中点，DM平分∠ADC，则AM平分∠DAB吗？试说明理由。（提示：过点M作ME垂直AD于E）。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，△ABC三个顶点坐标分别为A（﹣2，4），B（﹣2，1），C（﹣5，2）．
（1）请画出△ABC关于x轴对称的△A1B1C1．
（2）将△A1B1C1的三个顶点的横坐标与纵坐标同时乘以﹣2，得到对应的点A2，B2，C2，请画出△A2B2C2．
（3）求△A1B1C1与△A2B2C2的面积比．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一次物理竞赛中,有一道四选二的双项选择题,评分标准是:多选或只要选错一项就不得分,只选一项且对得1分,全对得3分.
(1)小娟在不会做的情况下,根据题意决定任选一项作为答案,求她得到1分的概率.
(2)小娜在不会做的情况下,根据题意决定任选两项作答案,用列表法表示小娜答案的所有可能结果,并求她得到3分的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】作图题:如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（﹣2，1），B（﹣1，4），C（﹣3，2）．
(1)画出△ABC关于y轴对称的图形△A1B1C1，并直接写出C1点坐标；
(2)以原点O为位似中心，位似比为1：2，在y轴的左侧，画出△ABC放大后的图形△A2B2C2，并直接写出C2点坐标；
(3)如果点D（a，b）在线段AB上，请直接写出经过（2）的变化后D的对应点D2的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移，使点A变换为点A′，点B′、C′分别是B、C的对应点．
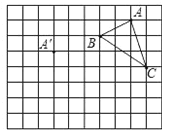
（1）请画出平移后的△A′B′C′，并求△A′B′C′的面积；
（2）若连接AA′，CC′，则这两条线段之间的关系是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列一元二次方程中，两实根之和为1的是 （ ）
A. x2—x＋1＝0 B. x2＋x—3＝0 C. 2 x2－x－1＝0 D. x2－x－5＝0
相关试题
