搜索
【题目】探究题：观察下列各式：①
；②
；③
.
（1）猜想
的变形结果并验证；
（2）针对上述各式反映的规律，给出用
（为任意自然数，且
）表示的等式，并进行证明.
参考答案：
【答案】（1）猜想
，验证见解析；（2）
，证明见解析
【解析】
（1）注意观察左边的被开方数是一个带分数，其分数部分的分子是1，分母比其整数部分大2．右边的结果根号外的比左边的整数部分大1，根号内的是左边的分数部分，据此写出猜想，然后利用二次根式的性质进行验证；
（2）注意观察左边的被开方数是一个带分数，其分数部分的分子是1，分母比其整数部分大2．右边的结果根号外的比左边的整数部分大1，根号内的是左边的分数部分，据此写出规律，然后利用二次根式的性质进行验证．
（1）猜想，
验证：左边
右边，故等式成立；
（2）根据规律可得：，
证明：左边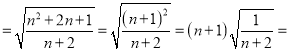
右边，
故等式成立.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂修建了甲、乙两个水池，最大蓄水量都是1200立方米，如果甲池有水480立方米，乙池蓄满水，甲池每小时进水80立方米，乙池每小时放水100立方米.
（1）分别写出甲、乙两池的水量
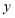与时间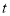
的函数解析式；（2）甲、乙两池同时进水、放水，经过几小时两个水池内的水一样多？
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列命题中，真命题的是（ ）
A.两边和一角对应相等，两三角形全等
B.两腰对应相等的两等腰三角形全等
C.两角和一边对应相等，两三角形全等
D.两锐角对应相等的两直角三角形全等
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）问题发现,
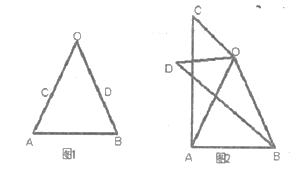
如图1，在
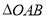中，
，
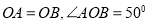是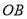
上一点，将点绕点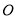
顺时针旋转50°得到点
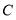，则
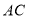与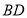
的数量关系是________________________。（2）类比探究
如图2，将（1）中的
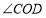绕点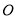在平面内旋转，（1）中的结论是否成立，并就图2的情形说明理由。（3）拓展延伸
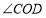绕点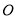在平面旋转，当旋转到
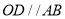时，请直接写出
度数。 -
科目： 来源： 题型：
查看答案和解析>>【题目】右图是老北京城一些地点的分布示意图．在图中，分别以正东、正北方向为
轴、
轴的正方向建立平面直角坐标系，有如下四个结论：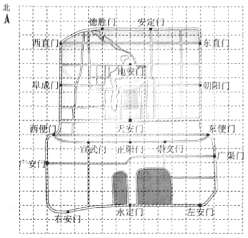
①当表示天安门的点的坐标为（0，0），表示广安门的点的坐标为（
，
）时，表示左安门的点的坐标为（5，）；②当表示天安门的点的坐标为（0，0），表示广安门的点的坐标为（
，）时，表示左安门的点的坐标为（10，）；③当表示天安门的点的坐标为（1，1），表示广安门的点的坐标为（
，
）时，表示左安门的点的坐标为（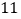
，）；④当表示天安门的点的坐标为（
，），表示广安门的点的坐标为（
，
）时，表示左安门的点的坐标为（
，）．上述结论中，所有正确结论的序号是
A. ①②③ B. ②③④ C. ①④ D. ①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两车分别从A，B两地同时出发，沿同一条公路相向而行，相遇时甲、乙所走路程的比为
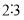，甲、乙两车离AB中点C的路程
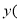千米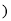
与甲车出发时间
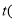时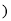的关系图象如图所示，则下列说法错误的是（ ）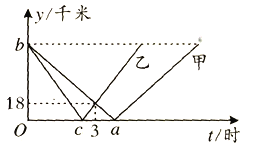 
A.A，B两地之间的距离为180千米
B.乙车的速度为36千米
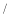时C.a的值为
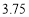
D.当乙车到达终点时，甲车距离终点还有30千米
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在矩形
中，
，
，点
、
分别在
、
上，
，现把一块直径为
的量角器（圆心为
）放置在图形上，使其
线
与
重合；若将量角器线上的端点
固定在点上，再把量角器绕点顺时针方向旋转
，此时量角器的半圆弧与相交于点
，设点处量角器的读数为
．
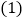用含的代数式表示
的大小；
当等于多少时，线段
与
平行？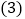
在量角器的旋转过程中，过点
作
，交
于点
，交
于点
．设
，
的面积为
，试求出关于
的函数关系式，并写出自变量的取值范围．
相关试题
