【题目】甲、乙两车分别从A,B两地同时出发,沿同一条公路相向而行,相遇时甲、乙所走路程的比为![]() ,甲、乙两车离AB中点C的路程
,甲、乙两车离AB中点C的路程![]() 千米
千米![]() 与甲车出发时间
与甲车出发时间![]() 时
时![]() 的关系图象如图所示,则下列说法错误的是( )
的关系图象如图所示,则下列说法错误的是( )
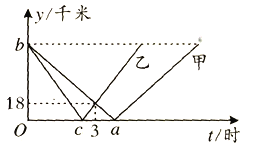
A.A,B两地之间的距离为180千米
B.乙车的速度为36千米![]() 时
时
C.a的值为![]()
D.当乙车到达终点时,甲车距离终点还有30千米
参考答案:
【答案】D
【解析】
根据两车相遇时甲、乙所走路程的比为2:3及两车相遇所用时间,即可求出A、B两地之间的距离;根据乙车的速度=相遇时乙车行驶的路程÷两车相遇所用时间,进而求出乙车的速度;根据甲车的速度=相遇时甲车行驶的路程÷两车相遇所用时间即可求出甲车的速度,然后根据时间=两地之间路程的一半÷甲车的速度,进而求出a值;根据时间=两地之间路程÷乙车的速度求出乙车到达终点所用时间,再求出该时间内甲车行驶的路程,用两地间的距离与甲车行驶的路程之差即可得出结论.
解:A、A、B两地之间的距离为18×2÷![]() =180(千米),所以A正确;
=180(千米),所以A正确;
B、乙车的速度为180![]() ÷3=36(千米/小时),所以B正确;
÷3=36(千米/小时),所以B正确;
C、甲车的速度为180![]() =24(千米/小时),
=24(千米/小时),
a的值为180÷2÷24=3.75,所以C正确;
D、乙车到达终点的时间为180÷36=5(小时),
甲车行驶5小时的路程为24×5=120(千米),
当乙车到达终点时,甲车距离终点距离为180﹣120=60(千米),所以D错误.
故选:D
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现,
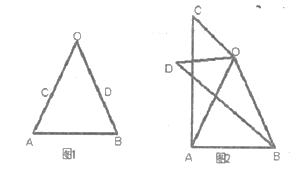
如图1,在
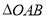 中,
中,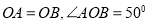 ,
, 是
是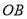 上一点,将点
上一点,将点 绕点
绕点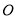 顺时针旋转50°得到点
顺时针旋转50°得到点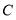 ,则
,则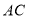 与
与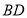 的数量关系是________________________。
的数量关系是________________________。(2)类比探究
如图2,将(1)中的
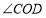 绕点
绕点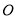 在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。
在平面内旋转,(1)中的结论是否成立,并就图2的情形说明理由。(3)拓展延伸
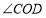 绕点
绕点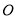 在平面旋转,当旋转到
在平面旋转,当旋转到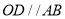 时,请直接写出
时,请直接写出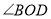 度数。
度数。 -
科目: 来源: 题型:
查看答案和解析>>【题目】探究题:观察下列各式:①
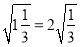 ;②
;②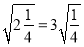 ;③
;③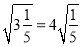 .
.(1)猜想
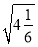 的变形结果并验证;
的变形结果并验证;(2)针对上述各式反映的规律,给出用
 (
( 为任意自然数,且
为任意自然数,且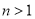 )表示的等式,并进行证明.
)表示的等式,并进行证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】右图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为
 轴、
轴、 轴的正方向建立平面直角坐标系,有如下四个结论:
轴的正方向建立平面直角坐标系,有如下四个结论: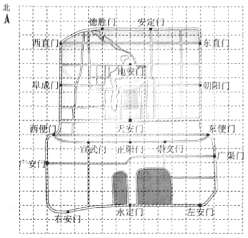
①当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(
 ,
, )时,表示左安门的点的坐标为(5,
)时,表示左安门的点的坐标为(5, );
);②当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(
 ,
, )时,表示左安门的点的坐标为(10,
)时,表示左安门的点的坐标为(10, );
);③当表示天安门的点的坐标为(1,1),表示广安门的点的坐标为(
 ,
, )时,表示左安门的点的坐标为(
)时,表示左安门的点的坐标为( ,
, );
);④当表示天安门的点的坐标为(
 ,
, ),表示广安门的点的坐标为(
),表示广安门的点的坐标为( ,
, )时,表示左安门的点的坐标为(
)时,表示左安门的点的坐标为( ,
, ).
).上述结论中,所有正确结论的序号是
A. ①②③ B. ②③④ C. ①④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
, ,点
,点 、
、 分别在
分别在 、
、 上,
上, ,现把一块直径为
,现把一块直径为 的量角器(圆心为
的量角器(圆心为 )放置在图形上,使其
)放置在图形上,使其 线
线 与
与 重合;若将量角器
重合;若将量角器 线上的端点
线上的端点 固定在点
固定在点 上,再把量角器绕点
上,再把量角器绕点 顺时针方向旋转
顺时针方向旋转 ,此时量角器的半圆弧与
,此时量角器的半圆弧与 相交于点
相交于点 ,设点
,设点 处量角器的读数为
处量角器的读数为 .
.
 用含
用含 的代数式表示
的代数式表示 的大小;
的大小; 当
当 等于多少时,线段
等于多少时,线段 与
与 平行?
平行?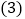 在量角器的旋转过程中,过点
在量角器的旋转过程中,过点 作
作 ,交
,交 于点
于点 ,交
,交 于点
于点 .设
.设 ,
, 的面积为
的面积为 ,试求出
,试求出 关于
关于 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正方形ABCD绕点A逆时针旋转30°得到AB′C′D′,如果AB=1,点C与C′的距离为( )

A.
 B.
B.  ﹣
﹣ C. 1 D.
C. 1 D.  ﹣1
﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;②△HED的面积是1﹣
 ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG=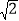 .其中正确的结论是( )
.其中正确的结论是( )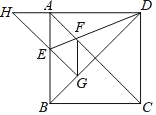
A. ①②③ B. ①②④ C. ①③④ D. ②③④
相关试题

