【题目】如图,平面直角坐标系中O是原点,ABCD的顶点A,C的坐标分别是(8,0),(3,4),点D,E把线段OB三等分,延长CD、CE分别交OA、AB于点F,G,连接FG.则下列结论:
①F是OA的中点;②△OFD与△BEG相似;③四边形DEGF的面积是 ![]() ;④OD=
;④OD= ![]()
其中正确的结论是(填写所有正确结论的序号).
参考答案:
【答案】②③
【解析】解:①∵四边形OABC是平行四边形,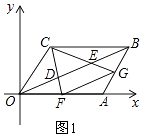
∴BC∥OA,BC=OA,
∴△CDB∽△FDO,
∴ ![]() ,
,
∵D、E为OB的三等分点,
∴ ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴BC=2OF,
∴OA=2OF,
∴F是OA的中点;
所以①结论正确;②如图2,延长BC交y轴于H,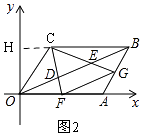
由C(3,4)知:OH=4,CH=3,
∴OC=5,
∴AB=OC=5,
∵A(8,0),
∴OA=8,
∴OA≠AB,
∴∠AOB≠∠EBG,
∴△OFD∽△BEG不成立,
所以②结论不正确;③由①知:F为OA的中点,
同理得;G是AB的中点,
∴FG是△OAB的中位线,
∴FG= ![]() ,FG∥OB,
,FG∥OB,
∵OB=3DE,
∴FG= ![]() DE,
DE,
∴ ![]() =
= ![]() ,
,
过C作CQ⊥AB于Q,
SOABC=OAOH=ABCQ,
∴4×8=5CQ,
∴CQ= ![]() ,
,
S△OCF= ![]() OFOH=
OFOH= ![]() ×4×4=8,
×4×4=8,
S△CGB= ![]() BGCQ=
BGCQ= ![]() ×
× ![]() ×
× ![]() =8,
=8,
S△AFG= ![]() ×4×2=4,
×4×2=4,
∴S△CFG=SOABC﹣S△OFC﹣S△OBG﹣S△AFG=8×4﹣8﹣8×4=12,
∵DE∥FG,
∴△CDE∽△CFG,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴ ![]() ,
,
∴S四边形DEGF= ![]() ;
;
所以③结论正确;④在Rt△OHB中,由勾股定理得:OB2=BH2+OH2 ,
∴OB= ![]() =
= ![]() ,
,
∴OD= ![]() ,
,
所以④结论不正确;
故本题结论正确的有:②③;
所以答案是:②③.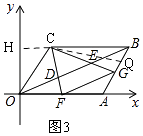
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择.李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家.设他出地铁的站点与文化宫距离为x(单位:千米),乘坐地铁的时间y1(单位:分钟)是关于x的一次函数,其关系如下表:
地铁站
A
B
C
D
E
x(千米)
8
9
10
11.5
13
y1(分钟)
18
20
22
25
28
(1)求y1关于x的函数表达式;
(2)李华骑单车的时间y2(单位:分钟)也受x的影响,其关系可以用y2=
 x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间.
x2-11x+78来描述,请问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短?并求出最短时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】若不等式-1≤x<a有4个整数解,则a的取值范围是( ).
A. 1≤a<2 B. 1<a<2 C. 2<a≤3 D. 2<a<3
-
科目: 来源: 题型:
查看答案和解析>>【题目】若ab2=﹣6,则﹣ab2(a2b4﹣ab2﹣1)的值为( )
A.246
B.216
C.﹣216
D.274 -
科目: 来源: 题型:
查看答案和解析>>【题目】商店为了对某种商品促销,将定价为3元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折.如果用27元钱,最多可以购买该商品的件数是_____.
-
科目: 来源: 题型:
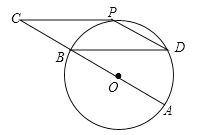
查看答案和解析>>【题目】如图,⊙O的直径AB=12cm,C为AB延长线上一点,CP与⊙O相切于点P,过点B作弦BD∥CP,连接PD.
(1)求证:点P为
 的中点;
的中点;(2)若∠C=∠D,求四边形BCPD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:2(x-1)-3(2+x)=5
相关试题

