【题目】计算.
(1)![]() y=2y﹣1
y=2y﹣1
(2)5(x﹣5)+2(x﹣12)=0
(3)y﹣![]() =1﹣
=1﹣![]()
(4)2(x﹣2)﹣(4x﹣1)=3(1﹣x)
(5)![]()
(6)![]() .
.
参考答案:
【答案】(1) y=1 (2) x=7 (3) y=![]() (4) x=6 (5) x=4 (6) x=
(4) x=6 (5) x=4 (6) x=![]()
【解析】(1)根据一元一次方程的解法:去分母,移项,合并同类项,系数化为1,解方程即可;
(2)根据一元一次方程的解法:去括号,移项,合并同类项,系数化为1,解方程即可;
(3)根据一元一次方程的解法:去分母,去括号,移项,合并同类项,系数化为1,解方程即可;
(4)根据一元一次方程的解法:去括号,移项,合并同类项,系数化为1,解方程即可;
(5)根据一元一次方程的解法:去分母,去括号,移项,合并同类项,系数化为1,解方程即可;
(6)先根据分数的基本性质化简方程,再根据一元一次方程的解法:去分母,去括号,移项,合并同类项,系数化为1,解方程即可;
(1)![]() y=2y﹣1,
y=2y﹣1,
5﹣2y=6y﹣3,
5+3=6y+2y,
8y=8,
y=1;
(2)5(x﹣5)+2(x﹣12)=0,
5x﹣25+2x﹣24=0,
5x+2x=25+24,
7x=49,
x=7;
(3)y﹣![]() =1﹣
=1﹣![]() ,
,
6y﹣3(y﹣1)=6﹣(y+2),
6y﹣3y+3=6﹣y﹣2,
6y﹣3y+y=6﹣2﹣3,
4y=1,
y=![]() ;
;
(4)2(x﹣2)﹣(4x﹣1)=3(1﹣x),
2x﹣4﹣4x+1=3﹣3x,
2x﹣4x+3x=3+4﹣1,
x=6;
(5)![]() ,
,
2(x﹣1)﹣(x+2)=3(4﹣x),
2x﹣2﹣x﹣2=12﹣3x,
2x﹣x+3x=12+2+2,
4x=16,
x=4;
(6)![]()
![]()
78﹣10(3+2x)=15(x﹣5),
78﹣30﹣2x=15x﹣75,
78﹣30+75=15x+2x,
123=17x,
x=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为( ).

A.2
 B.4
B.4 C.4 D.8
C.4 D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
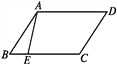
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径是8,AB是⊙O的直径,M为AB上一动点,
 =
=  =
=  ,则CM+DM的最小值为 .
,则CM+DM的最小值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G、F,H为CG的中点,连接DE、EH、DH、FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若
 =
=  ,则3S△EDH=13S△DHC , 其中结论正确的有(填写序号).
,则3S△EDH=13S△DHC , 其中结论正确的有(填写序号). 
-
科目: 来源: 题型:
查看答案和解析>>【题目】提出命题:如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.
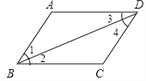
小明提供了如下解答过程:
证明:连接BD.
∵∠1+∠3=180-∠A,∠2+∠4=180―∠C,∠A=∠C,
∴ ∠1+∠3=∠2+∠4.
∵∠ABC=∠ADC,
∴∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,说明错在何处,并给出正确的证明过程.
(2)用语言叙述上述命题:___________________________________________________.
运用探究:(3)下列条件中,能确定四边形ABCD是平行四边形的是(_____)
A. ∠A∶∠B∶∠C∶∠D=1∶2∶3∶4 B. ∠A∶∠B∶∠C∶∠D=1∶3∶1∶3
C. ∠A∶∠B∶∠C∶∠D=2∶3∶3∶2 D. ∠A∶∠B∶∠C∶∠D=1∶1∶3∶3
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣64的立方根是( )
A.±8B.4C.﹣4D.16
相关试题

