【题目】在![]() 中,点
中,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,根据下列给定的条件,不能判断
上,根据下列给定的条件,不能判断![]() 与
与![]() 平行的是( )
平行的是( )
A. AD=6,BD=4,AE=2.4,CE=1.6
B. BD=2,AB=6,CE=1,AC=3;
C. AD=4,AB=6,DE=2,BC=3;
D. AD=4,AB=6,AE=2,AC=3.
参考答案:
【答案】C
【解析】根据平行线分线段成比例定理,分别求得各对应线段的比,比相等,即可判定DE与BC平行.注意排除法在解选择题中的应用.
如图所示,
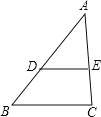
A,由AD=6,BD=4,得![]() ,由AE=2.4,CE=1.6,得
,由AE=2.4,CE=1.6,得![]() ,所以
,所以![]() ,所以△ADE∽△ABC,所以∠ADE=∠ABC,所以DE∥BC;
,所以△ADE∽△ABC,所以∠ADE=∠ABC,所以DE∥BC;
B,由DB=2,AB=6,得![]() ,由CE=1,AC=3得
,由CE=1,AC=3得![]() ,所以
,所以![]() ,所以△ADE∽△ABC,所以∠ADE=∠ABC,所以DE∥BC;
,所以△ADE∽△ABC,所以∠ADE=∠ABC,所以DE∥BC;
C,△ABC中,由AD=4,AB=6,得![]() ,由DE=2,BC=3得
,由DE=2,BC=3得![]() ,但是DE与BC不一定平行,(如下图);
,但是DE与BC不一定平行,(如下图);
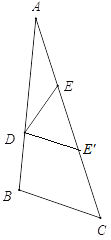
D,由AD=4,AB=6,得![]() ,由AE=2,AC=3得
,由AE=2,AC=3得![]() ,所以
,所以![]() ,所以△ADE∽△ABC,所以∠ADE=∠ABC,所以DE∥BC,
,所以△ADE∽△ABC,所以∠ADE=∠ABC,所以DE∥BC,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2-5x+c的图象如图所示,请根据图象回答下列问题:

(1) a=_______,c=______.
(2)函数图象的对称轴是_________,顶点坐标P__________.
(3)该函数有最______值,当x=______时,y最值=________.
(4)当x_____时,y随x的增大而减小. 当x_____时,y随x的增大而增大.
(5)抛物线与x轴交点坐标A_______,B________;与y轴交点C 的坐标为_______;
 =_________,
=_________, =________.
=________.(6)当y>0时,x的取值范围是_________;当y<0时,x的取值范围是_________.
(7)方程ax2-5x+c=0中△的符号为________.方程ax2-5x+c=0的两根分别为_____,____.
(8)当x=6时,y______0;当x=-2时,y______0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线L;y=ax2+bx+c(其中a、b、c都不等于0), 它的顶点P的坐标是
 ,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.
,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.(1)请直接写出抛物线y=2x2-4x+1的伴随抛物线和伴随直线的关系式:
伴随抛物线的关系式_________________
伴随直线的关系式___________________
(2)若一条抛物线的伴随抛物线和伴随直线分别是y=-x2-3和y=-x-3, 则这条抛物线的关系是___________:
(3)求抛物线L:y=ax2+bx+c(其中a、b、c都不等于0) 的伴随抛物线和伴随直线的关系式;
(4)若抛物线L与x轴交于A(x1,0),B(x2,0)两点x2>x1>0,它的伴随抛物线与x 轴交于C,D两点,且AB=CD,请求出a、b、c应满足的条件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一位篮球运动员在离篮圈水平距离为4m处跳起投篮,球沿一条抛物线运行,当球运行的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心离地面距离为3.05m.
(1)建立如图所示的直角坐标系,求抛物线所对应的函数关系式;
(2)若该运动员身高1.8m,这次跳投时,球在他头顶上方0.25m处出手.问:球出手时,他跳离地面多高?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在﹣2,3,﹣4,﹣5,6这五个数中,任取两个数相乘所得的积最大的是( )
A. 10B. 20C. ﹣30D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】班长去商店买贺卡50张,每张标价2元,若按标价的九折优惠,则班长应付( )
A. 45元B. 100元C. 10元D. 90元
-
科目: 来源: 题型:
查看答案和解析>>【题目】若某个证书的两个平方根是a-3与a+5,则a=_________.
相关试题

