Question

【题目】已知抛物线L;y=ax2+bx+c(其中a、b、c都不等于0), 它的顶点P的坐标是,与y轴的交点是M(0,c)我们称以M为顶点,对称轴是y轴且过点P的抛物线为抛物线L的伴随抛物线,直线PM为L的伴随直线.

(1)请直接写出抛物线y=2x2-4x+1的伴随抛物线和伴随直线的关系式:

伴随抛物线的关系式_________________

伴随直线的关系式___________________

(2)若一条抛物线的伴随抛物线和伴随直线分别是y=-x2-3和y=-x-3, 则这条抛物线的关系是___________:

(3)求抛物线L:y=ax2+bx+c(其中a、b、c都不等于0) 的伴随抛物线和伴随直线的关系式;

(4)若抛物线L与x轴交于A(x1,0),B(x2,0)两点x2>x1>0,它的伴随抛物线与x 轴交于C,D两点,且AB=CD,请求出a、b、c应满足的条件.

Answer 1

【答案】(1)y=-2x2+1,y=-2x+1. (2)y=x2-2x-3；（3）y=x+c；（4）b2=8ac且ab<0,(或b2=8ac且bc<0).

【解析】本题主要考查了二次函数与一元二次方程的关系以及一元二次方程根与系数的关系．

（1）先根据抛物线的解析式求出其顶点P和抛物线与y轴的交点M的坐标．然后根据M的坐标用顶点式二次函数通式设伴随抛物线的解析式然后将P点的坐标代入抛物线的解析式中即可求出伴随抛物线的解析式．根据M，P两点的坐标即可求出直线PM的解析式；

（2）由题意可知：伴随抛物线的顶点坐标是抛物线与y轴交点坐标，伴随抛物线与伴随直线的交点（与y轴交点除外）是抛物线的顶点，据此可求出抛物线的解析式；

（3）方法同（1）；

（4）本题要考虑的a、b、c满足的条件有：

抛物线和伴随抛物线都与x轴有两个交点，因此△＞0，①

由于抛物线L中，x2＞x1＞0，因此抛物线的对称轴x＞0，两根的积大于0．②

根据两抛物线的解析式分别求出AB、CD的长，根据AB=CD可得出另一个需满足的条件…③综合这三种情况即可得出所求的a、b、c需满足的条件．

解：(1)y=-2x2+1,y=-2x+1.

(2)y=x2-2x-3

(3)∵伴随抛物线的顶点是(0,c),

∴设它的解析式为y=m(x-0)2+c(m≠0).

∴设抛物线过P,

∴

解得m=-a,∴伴随抛物线关系式为y=-ax2+c.

设伴随直线关系式为y=kx+c(k≠0).

∵P在此直线上,∴, ∴k=.

∴伴随直线关系式为y=x+c

(4)∵抛物线L与x轴有两交点,∴△1=b2-4ac>0,∴b2<4ac.

∵x2>x1>0,∴x1+ x2= ->0,x1x2=>0,∴ab<0,ac>0.

对于伴随抛物线y=-ax2+c,有△2=02-(-4ac)=4ac>0.由-ax2+c=0,得x=.

∴,∴CD=2.

又AB=x2-x1=.

由AB=CD,得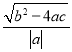=2, 整理得b2=8ac,

综合b2>4ac,ab<0,ac>0,b2=8ac,得a,b,c满足的条件为b2=8ac且ab<0,(或b2=8ac且bc<0).