【题目】如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,AD与OC交于点E,连接CD、OD,给出以下四个结论: ①AC∥OD;②CE=OE;③∠CDE=∠COD;④2CD2=CEAB.
其中正确结论的序号是(在横线上填上你认为所有正确结论的代号).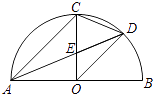
参考答案:
【答案】①③④
【解析】解:∵AB是半圆直径, ∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO= ![]() ∠CAB,
∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,故①正确.
由题意得,OD=R,AC= ![]() R,
R,
∵OE:CE=OD:AC= ![]() ,
,
∴OE≠CE,故②错误;
∵AB是半圆直径,半径OC⊥AB于点O,
∴∠AOC=∠COB=90°,
∴∠CDE= ![]() ∠AOC=45°,
∠AOC=45°,
∵OA=OC,
∴∠CAO=45°,
∵AD平分∠CAB交弧BC于点D,
∴∠DAO=22.5°,
∴∠COD=2∠CAD=45°,
∴∠CDE=∠COD;故③正确;
∵AD平分∠CAB交弧BC于点D,
∴∠CAD= ![]() ×45°=22.5°,
×45°=22.5°,
∴∠COD=45°,
∵AB是半圆直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°
∵∠CAD=∠ADO=22.5°(已证),
∴∠CDE=∠ODC﹣∠ADO=67.5°﹣22.5°=45°,
∴△CED∽△CDO,
∴ ![]() ,
,
∴CD2=COCE= ![]() ABCE,
ABCE,
∴2CD2=CEAB,故④正确.
综上可得①③④正确.
所以答案是:①③④,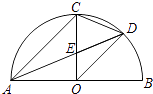
【考点精析】通过灵活运用圆周角定理和相似三角形的判定与性质,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角△ABC沿MN所在的直线以2cm/min的速度向右作匀速运动.如果MN=2AC=4cm,那么△ABC和正方形XYMN重叠部分的面积S(cm2)与匀速运动所用时间t(min)之间的函数的大致图像是( )
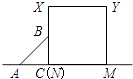
A.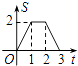
B.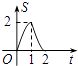
C.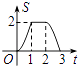
D.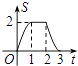
-
科目: 来源: 题型:
查看答案和解析>>【题目】某自行车厂一周计划生产1050辆自行车,平均每天生产150辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):

(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比产量最少的一天多生产 辆;
(3)该厂实行计件工资制,每辆车50元,超额完成任务每辆奖10元,少生产一辆扣10元,那么该厂工人这一周的工资总额是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)(-78) +(+5)+(+78) (2)(+23)+(-17)+(+6)+(-22)
(3)[45-(
 -
-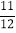 +
+ )×36]÷5 (4)99
)×36]÷5 (4)99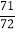 ×(-36)
×(-36) -
科目: 来源: 题型:
查看答案和解析>>【题目】每个小方格是边长为1个单位长度的小正方形,菱形OABC在平面直角坐标系的位置如图所示.
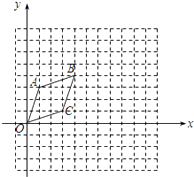
(I)以O为位似中心,在第一象限内将菱形OABC放大为原来的2倍得到菱形OA1B1C1 , 请画出菱形OA1B1C1 , 并直接写出点B1的坐标;
(II)将菱形OABC绕原点O顺时针旋转90°菱形OA2B2C2 , 请画出菱形OA2B2C2 , 并求出点B旋转到点B2的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,点E是BC上一点,直线AE交BD于点M,交DC的延长线于点F,G是EF的中点,连结CG.求证: ①△ABM≌△CBM;
②CG⊥CM.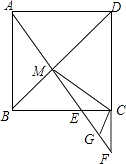
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知有理数a,b满足ab<0,a+b>0,7a+2b+1=﹣|b﹣a|,则
 的值为_____.
的值为_____.
相关试题

