【题目】如图,在平面直角坐标系中, ![]() ,
, ![]() ∥
∥![]() 轴,
轴, ![]() .
.

⑴.求点![]() 的坐标:
的坐标:
⑵.四边形![]() 的面积
的面积![]() 四边形
四边形![]() ;
;
⑶. 在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() △
△![]() =
= ![]() 四边形
四边形![]() ;若存在,求出点
;若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() (2)7(3)点
(2)7(3)点![]() 的坐标为
的坐标为![]() 或
或![]()
【解析】试题分析:⑴抓住![]() ∥
∥![]() 轴,可以推出
轴,可以推出![]() 纵坐标相等,而
纵坐标相等,而![]() 是
是![]() 横坐标之差的绝对值,以此可以求出点
横坐标之差的绝对值,以此可以求出点![]() 的坐标,根据图示要舍去一种情况.
的坐标,根据图示要舍去一种情况.
⑵四边形![]() 是梯形,根据点的坐标可以求出此梯形的上、下底和高,面积可求.
是梯形,根据点的坐标可以求出此梯形的上、下底和高,面积可求.
⑶存在性问题可以先假设存在,在假设的基础上以![]() △
△![]() =
= ![]() 四边形
四边形![]() 为等量关系建立方程,以此来探讨在
为等量关系建立方程,以此来探讨在![]() 轴上是否存在着符合条件的点
轴上是否存在着符合条件的点![]() .
.
试题解析:⑴.∵![]() ∥
∥![]() 轴, ∴
轴, ∴![]() 纵坐标相等;
纵坐标相等;
∵![]() ∴点
∴点![]() 的纵坐标也为2.
的纵坐标也为2.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
又![]() ,且
,且![]() ,
,
∴![]() ,解得:
,解得: ![]() .
.
由于点![]() 在第一象限,所以
在第一象限,所以![]() ,所以
,所以![]() 的坐标为
的坐标为![]() .
.
⑵.∵![]() ∥
∥![]() 轴,且
轴,且![]()
∴![]()
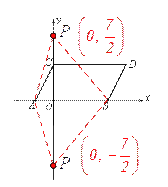
∴![]() 四边形
四边形![]() =
= ![]() .
.
⑶.假设在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() △
△![]() =
= ![]() 四边形
四边形![]() .
.
设![]() 的坐标为
的坐标为![]() ,则
,则![]() ,而
,而![]()
∴![]() △
△![]() =
=![]() .
.
∵![]() △
△![]() =
= ![]() 四边形
四边形![]() ,
, ![]() 四边形
四边形![]()
![]()
∴![]() ,解得;
,解得; ![]() .均符合题意.
.均符合题意.
∴在![]() 轴上存在点
轴上存在点![]() ,使
,使![]() △
△![]() =
= ![]() 四边形
四边形![]() .
.
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读:若一个三角形的三边长分别为a、b、c,设
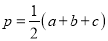 ,
,则这个三角形的面积为
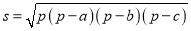 .
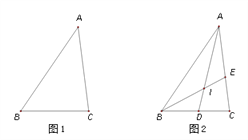
.(2)应用:如图1,在△ABC中,AB=6,AC=5,BC=4,求△ABC面积.
(3)引申:如图2,在(2)的条件下,AD、BE分别为△ABC的角平分线,它们的交点为I,求I到AB的距离.
-
科目: 来源: 题型:
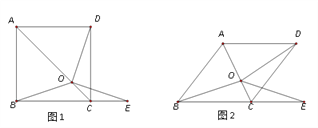
查看答案和解析>>【题目】如图1,在正方形ABCD中,O是对角线AC上一点,点E在BC的延长线上,且OE = OB.
(1)求证:△OBC ≌ △ODC.
(2)求证:∠DOE = ∠ABC.
(3)把正方形ABCD改为菱形,其他条件不变(如图2),若∠ABC = 52° ,求∠DOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“震灾无情人有情”.民政局将全市为四川受灾地区捐赠的物资打包成件,其中帐篷和食品共320件,帐篷比食品多80件.
(1)求打包成件的帐篷和食品各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批帐篷和食品全部运往受灾地区.已知甲种货车最多可装帐篷40件和食品10件,乙种货车最多可装帐篷和食品各20件.则民政局安排甲、乙两种货车时有几种方案?请你帮助设计出来.
(3)在第(2)问的条件下,如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元.民政局应选择哪种方案可使运输费最少?最少运输费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
(1)从小刚家到该景区乘车一共用了多少时间?
(2)求线段AB对应的函数解析式;
(3)小刚一家出发2.5小时时离目的地多远?

-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式a3﹣6a2+9a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】禽流感病毒的形状一般为球形,直径大约为0.000000102m,该直径用科学记数法表示为m.
相关试题

