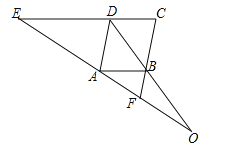
【题目】如图,已知EC∥AB,∠EDA=∠ABF.
(1)求证:四边形ABCD是平行四边形;
(2)求证:![]() =OEOF.
=OEOF.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)由EC∥AB,∠EDA=∠ABF,可证得∠DAB=∠ABF,即可证得AD∥BC,则得四边形ABCD为平行四边形;
(2)由EC∥AB,可得![]() ,由AD∥BC,可得
,由AD∥BC,可得![]() ,等量代换得出
,等量代换得出![]() ,即
,即![]() =OEOF.
=OEOF.
试题解析:(1)∵EC∥AB,∴∠EDA=∠DAB,∵∠EDA=∠ABF,∴∠DAB=∠ABF,∴AD∥BC,∵DC∥AB,∴四边形ABCD为平行四边形;
(2)∵EC∥AB,∴△OAB∽△OED,∴![]() ,∵AD∥BC,∴△OBF∽△ODA,∴
,∵AD∥BC,∴△OBF∽△ODA,∴![]() ,∴
,∴![]() ,∴
,∴![]() =OEOF.
=OEOF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆轿车和一辆货车分别从甲、乙两地同时出发,匀速相向而行,相遇后继续前行,已知两车相遇时轿车比货车多行驶了90千米,设行驶的时间为x(小时),两车之间的距离为y(千米),图中的折线表示从两车出发至轿车到达乙地这一过程中y与x之间的函数关系.根据图像提供的信息,解答下列问题:
(1)求线段AB所在直线的函数关系式,并求甲、乙两地的距离;
(2)求两车的速度;
(3)求点C的坐标,并写出点C的实际意义.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某一出租车一天下午以新合作超市为出发地在东西方向营运,向东为正,向西为负,行车里程(单位km),依先后次序记录如下:+7,-4,-6,+4,-8,+6,-3,-7,-5,+10.
⑴将最后一名乘客送到目的地,出租车离出发点多远?在新合作的什么方向?
⑵若每千米按2.4元收费,该司机一个下午的收入多少?
-
科目: 来源: 题型:
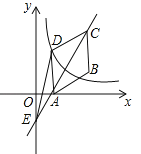
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线
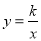 (k≠0,x>0)过点D.
(k≠0,x>0)过点D.(1)求双曲线的解析式;
(2)作直线AC交y轴于点E,连结DE,求△CDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】PM2.5是指大气中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2=2x的根为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=2x-3向上平移5个单位可得______直线.
相关试题

