【题目】如图,五边形ABCDE中,AB⊥BC,AE∥CD,∠A=∠E=120°,AB=CD=1,AE=2,则五边形ABCDE的面积等于. 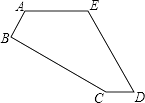
参考答案:
【答案】![]()
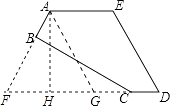
【解析】解:延长DC,AB交于点F,作AG∥DE交DF于点G. ∵AE∥CD,∠A=∠E=120°,
∴四边形AFDE是等腰梯形,且∠F=∠D=60°,△AFG是等边三角形,四边形AGDE是平行四边形.
设BF=x,
∵在直角△BCF中,∠BCF=90°﹣∠F=30°
∴FC=2x,
∴FD=2x+1.
∵平行四边形AGDE中,DG=AE=2,
∴FG=2x﹣1,
∵△AFG是等边三角形中,AF=FG,
∴x+1=2x﹣1,
解得:x=2.
在直角△BCF中,BC=BFtanF=2 ![]() ,
,
则S△BCF= ![]() BFBC=
BFBC= ![]() ×2×2
×2×2 ![]() =2
=2 ![]() .
.
作AH⊥DF于点H.
则AH=AFsinF=3× ![]() =
= ![]() ,
,
则S梯形AFDE= ![]() (AE+DF)AH=
(AE+DF)AH= ![]() ×(2+5)
×(2+5) ![]() =
= ![]() .
.
∴S五边形ABCDE=S梯形AFDE﹣S△BCF= ![]() ﹣2
﹣2 ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用含30度角的直角三角形和勾股定理的概念的相关知识可以得到问题的答案,需要掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.

(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(Ⅱ)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】对于坐标平面内的点,现将该点向右平移1个单位,再向上平移2的单位,这种点的运动称为点A的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5),已知点A的坐标为(1,0).

(1)分别写出点A经1次,2次斜平移后得到的点的坐标.
(2)如图,点M是直线l上的一点,点A关于点M的对称点的点B,点B关于直线l的对称轴为点C.
①若A、B、C三点不在同一条直线上,判断△ABC是否是直角三角形?请说明理由.
②若点B由点A经n次斜平移后得到,且点C的坐标为(7,6),求出点B的坐标及n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C是反比例函数y=
 (k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )
(k<0)图象上三点,作直线l,使A、B、C到直线l的距离之比为3:1:1,则满足条件的直线l共有( )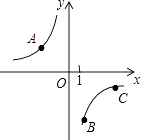
A.4条
B.3条
C.2条
D.1条 -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算: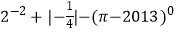 ;
;
(2)化简: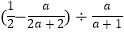 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)解方程:
(2)解不等式组: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点
的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是【 】

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
相关试题

