【题目】如图,一次函数y=﹣x+5的图象与反比例函数y= ![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.
(1)求反比例函数的解析式与点B坐标;
(2)求△AOB的面积;
(3)在第一象限内,当一次函数y=﹣x+5的值小于反比例函数y= ![]() (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围.
参考答案:
【答案】
(1)解:∵一次函数y=﹣x+5的图象过点A(1,n),
∴n=﹣1+5,解得:n=4,
∴点A的坐标为(1,4).
∵反比例函数y= ![]() (k≠0)过点A(1,4),
(k≠0)过点A(1,4),
∴k=1×4=4,
∴反比例函数的解析式为y= ![]() .
.
联立  ,解得:
,解得: ![]() 或
或 ![]() ,
,
∴点B的坐标为(4,1).
(2)解:延长AB交x轴与点C,则C(5,0),如图所示.


∵A(1,4),B(4,1),
∴S△AOB=S△AOC﹣S△BOC= ![]() OCyA﹣
OCyA﹣ ![]() OCyB=10﹣
OCyB=10﹣ ![]() =
= ![]()
(3)解:观察函数图象,发现:
当0<x<1或x>4时,反比例函数图象在一次函数图象上方,
∴当一次函数y=﹣x+5的值小于反比例函数y= ![]() (k≠0)的值时,x的取值范围为0<x<1或x>4.
(k≠0)的值时,x的取值范围为0<x<1或x>4.
【解析】(1)可通过一次函数先求出A坐标,代入双曲线解析式可求出反比例函数的解析式,再联立两个解析式组成的方程组,可求出B点坐标;(3)可数形结合,在交点两侧对应的x的范围,注意左侧无限趋近于y轴,进而范围为0<x<1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.
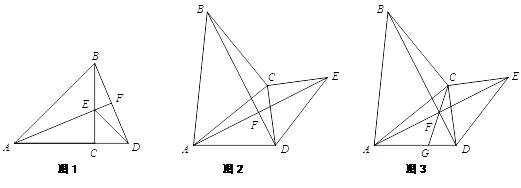
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5.
①求证:AF⊥BD,
②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时.求证:AF⊥BD;
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数,若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在A,B两地之间有汽车站C站,客车由A地驶往C站,货车由B地驶往A地.两车同时出发,匀速行驶.图2是客车、货车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.

(1)填空:A,B两地相距千米;
(2)求两小时后,货车离C站的路程y2与行驶时间x之间的函数关系式;
(3)当客车行驶多长时间,客、货两车相距150千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( )
A.原点的坐标是(0,0)
B.x轴上的所有点的纵坐标都相等
C.y轴上的所有点的横坐标都相等
D.点(0,﹣1)在第四象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市从今年1月1日起调整水价,每立方米水费上涨了原价的
 .据了解,某校去年11月份的水费是1800元,而今年1月份的水费是3600元.如果该校今年1月份的用水量比去年11月份的用水量多600m3 .
.据了解,某校去年11月份的水费是1800元,而今年1月份的水费是3600元.如果该校今年1月份的用水量比去年11月份的用水量多600m3 .
(1)该市原来每立方米水价是多少元?
(2)该校开展了“节约每一滴水”的主题活动,采取了有效的节约用水措施,计划今年5月份的用水量较1月份降低20%,那么该校今年5月份应交的水费是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,属于假命题的是( )
A. 三角形的内角和等于180°; B. 圆是轴对称图形,任何一条直径都是圆的对称轴;
C. 对顶角相等; D. 在同一平面内,垂直于同一条直线的两条直线相互平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在正方形ABCD中,AB=1,
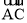 是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作
是以点B为圆心,AB长为半径的圆的一段弧,点E是边AD上的动点(点E与点A,D不重合),过E作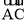 所在圆的切线,交边DC于点F,G为切点.
所在圆的切线,交边DC于点F,G为切点.(1)求证:EA=EG;
(2)设AE=x,FC=y,求y关于x的函数关系式,并直接写出x的取值范围;
(3)如图2所示,将△DEF沿直线EF翻折后得△D1EF,连接AD1,D1D,试探索:当点E运动到何处时,△AD1D与△ED1F相似?请说明理由.
相关试题

