【题目】如图所示,∠AOB=41°,点P为∠AOB内的一点,分别作出P点关于OA,OB的对称点![]() ,
,![]() ,连接
,连接![]() 交OA于M,交OB于N,
交OA于M,交OB于N,![]() ,则△PMN的周长为_________,∠MPN
,则△PMN的周长为_________,∠MPN![]() ________°.
________°.

参考答案:
【答案】15 96°
【解析】
P点关于OA的对称是点P1,P点关于OB的对称点P2,故有PM=P1M,PN=P2N,据此可求得![]() 的周长, 根据等腰三角形的性质可得∠P1OA=∠POA,∠P2OB=∠POB,进而可得
的周长, 根据等腰三角形的性质可得∠P1OA=∠POA,∠P2OB=∠POB,进而可得![]() 的度数.
的度数.
解:∵P点关于OA的对称是点P1,P点关于OB的对称点P2,
∴PM=P1M,PN=P2N.
∴△PMN的周长为PM+PN+MN=MN+P1M+P2N=P1P2=15.
∵P点关于OA的对称是点P1,P点关于OB的对称点P2,
∴OA垂直平分P P1,OB垂直平分P P2
∴PM=P1M,PN=P2N.
∴∠PMN=2∠P1,∠PNM=2∠P2,
∵PP1⊥OA, PP2⊥OB,,
∴∠P2 P P1=180°-∠AOB=138°,
∴∠P1+∠P2=42°
∴∠MPN=180°-42°×2=96°
故答案为:15, 96°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=3,BC=4,AC=2,D、E、F分别为AB、BC、AC中点,连接DF、FE,则四边形DBEF的周长是( )

A.5
B.7
C.9
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】三张背面完全相同的数字牌,它们的正面分别印有数字“1”、“2”、“3”,将它们背面朝上,洗匀后随机抽取一张,记录牌上的数字并把牌放回,再重复这样的步骤两次,得到三个数字a、b、c,则以a、b、c为边长正好构成等边三角形的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣2,0)、B(1,0),直线x=﹣0.5与此抛物线交于点C,与x轴交于点M,在直线上取点D,使MD=MC,连接AC、BC、AD、BD,某同学根据图象写出下列结论:
①a﹣b=0;
②当﹣2<x<1时,y>0;
③四边形ACBD是菱形;
④9a﹣3b+c>0
你认为其中正确的是( )
A.②③④
B.①②④
C.①③④
D.①②③ -
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现在平均每天比原计划多生产 50 台机器,现在生产 600 台机器所需时间与原计划生产 450 台机器所需时间相同.
(1)现在平均每天生产多少台机器;
(2)生产 3000 台机器,现在比原计划提前几天完成.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、C把
 分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=1,则图中阴影部分的面积是 .
分成三等分,ED是⊙O的切线,过点B、C分别作半径的垂线段,已知∠E=45°,半径OD=1,则图中阴影部分的面积是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
例:已知:
 ,
,求:
 和
和  的值.
的值.解:

 ,
,
 ,
,
 ,
,
 ,
, ,
,
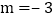 ,
, ,
,解决问题:
(1)若
 ,求 x、y 的值;
,求 x、y 的值;(2)已知
 ,
, ,
, 是
是  的三边长且满足
的三边长且满足  ,
,①直接写出a=__________.b=___________.
②若
 是
是  中最短边的边长(即c<a;c<b),且
中最短边的边长(即c<a;c<b),且  为整数,直接写出
为整数,直接写出  的值可能是 .
的值可能是 .
相关试题

