【题目】如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若∠C=60°,∠BED=70°.求∠ABC和∠BAC的度数. 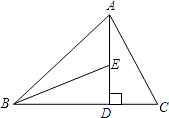
参考答案:
【答案】解:∵AD是△ABC的高, ∴∠ADB=90°.
又∵∠DBE+∠ADB+∠BED=180°,∠BED=70°,
∴∠DBE=180°﹣∠ADB﹣∠BED=20°.
∵BE平分∠ABC,
∴∠ABC=2∠DBE=40°.
又∵∠BAC+∠ABC+∠C=180°,∠C=60°,
∴∠BAC=180°﹣∠ABC﹣∠C=80°.
【解析】先根据AD是△ABC的高得出∠ADB=90°,再由三角形内角和定理及三角形外角的性质可知∠DBE+∠ADB+∠BED=180°,故∠DBE=180°﹣∠ADB﹣∠BED=20°.根据BE平分∠ABC得出∠ABC=2∠DBE=40°. 根据∠BAC+∠ABC+∠C=180°,∠C=60°即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小松调查了七年级(1)班50名同学最喜欢的篮球明星,结果如下:
B B C A A B C D C B C A D D B A C C B A
A B D A C C A B A C A B C D A C C A C A
A A A C A D B C C A
其中A代表科比,B代表库里,C代表詹姆斯,D代表格里芬,用扇形统计图表示该班同学最喜欢的篮球明星的情况,则表示喜欢科比的扇形的圆心角是(用度分秒表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】2011年国家启动实施农村义务教育学生营养改善计划,截至2014年4月,我省开展营养改善试点中小学达17580所,17580这个数用科学记数法可表示为( )
A. 17.58×103B. 175.8×104C. 1.758×105D. 1.758×104
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+x-1=0,则3x2+3x-5=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,点E是AB的中点,延长CB至D,使BD=
 BC.
BC. 
(1)用尺规作图的方法,过E点作EF⊥DC,垂足是点F;(不写作法,保留作图痕迹)
(2)求证:DF=CF. -
科目: 来源: 题型:
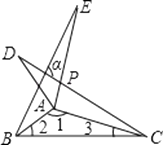
查看答案和解析>>【题目】如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为( )
A.80°
B.100°
C.60°
D.45° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
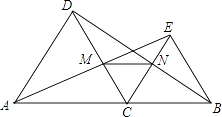
(1)求证:AE=BD;
(2)求证:MN∥AB.
相关试题

