【题目】某市开展了“雷锋精神你我传承,关爱老人从我做起”的主题活动,随机调查了本市部分老人与子女同住情况,根据收集到的数据,绘制成如下统计图表(不完整) 老人与子女同住情况百分比统计表
老人与子女 | 同住 | 不同住 | 不同住 | 其他 |
A | 50% | B | 5% |
根据统计图表中的信息,解答下列问题: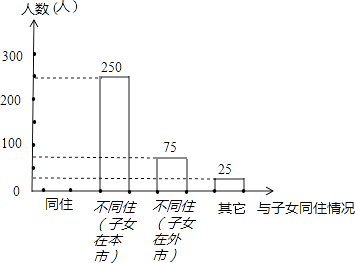
(1)求本次调查的老人的总数及a、b的值;
(2)将条形统计图补充完整;(画在答卷相对应的图上)
(3)若该市共有老人约15万人,请估计该市与子女“同住”的老人总数.
参考答案:
【答案】
(1)解:老人总数为250÷50%=500(人),
b= ![]() %=15%,
%=15%,
a=1﹣50%﹣15%﹣5%=30%
(2)解:如图:
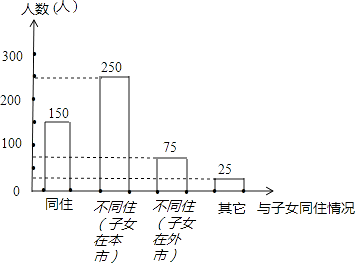
(3)解:该市与子女“同住”的老人的总数约为15×30%=4.5(万人).
【解析】(1)有统计图表中的信息可知:其他所占的比例为5%,又人数为25人,所以可以求出总人数,进而求出a和b的值;(2)有(1)的数据可将条形统计图补充完整;(3)用该老人的总数15万人乘以与子女“同住”所占的比例30%即为估计值.
【考点精析】根据题目的已知条件,利用条形统计图的相关知识可以得到问题的答案,需要掌握能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形,这个黑色菱形可分割成n个边长为1的小三角形,若
 =
= 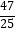 ,则△ABC的边长是 .
,则△ABC的边长是 . 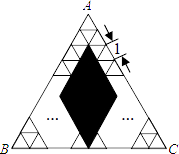
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在ABCD中,点F在AB的延长线上,且BF=AB,连接FD,交BC于点E.
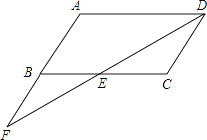
(1)说明△DCE≌△FBE的理由;
(2)若EC=3,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某品牌A,B两种型号冰箱的销售情况,王明对某专卖店一到七月份的销售情况进行了统计,并将得到的数据制成如下统计表:
月份
一月
二月
三月
四月
五月
六月
七月
A型销
售量(台)
10
14
17
16
13
14
14
B型销
售量(台)
6
10
14
15
16
17
20
完成下表:
平均数(台)
中位数(台)
方差
A型销售量
14
B型销售量
14
18.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】某药物研究单位试制成功一种新药,经测试,如果患者按规定剂量服用,那么服药后每毫升血液中含药量y(微克)随时间x(小时)之间的关系如图所示,如果每毫升血液中的含药量不小于20微克,那么这种药物才能发挥作用,请根据题意回答下列问题:
(1)服药后,大约 分钟后,药物发挥作用.
(2)服药后,大约 小时,每毫升血液中含药量最大,最大值是 微克;
(3)服药后,药物发挥作用的时间大约有 小时.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为进一步建设秀美、宜居的生态环境,某村欲购买甲、乙、丙三种树美化村庄,已知甲、乙丙三种树的价格之比为2:2:3,甲种树每棵200元,现计划用210000元资金,购买这三种树共1000棵.
(1)求乙、丙两种树每棵各多少元?
(2)若购买甲种树的棵树是乙种树的2倍,恰好用完计划资金,求这三种树各能购买多少棵?
(3)若又增加了10120元的购树款,在购买总棵树不变的前提下,求丙种树最多可以购买多少棵? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知菱形ABCD的边长为2
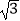 ,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(﹣
,点A在x轴负半轴上,点B在坐标原点.点D的坐标为(﹣ 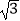 ,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.
,3),抛物线y=ax2+b(a≠0)经过AB、CD两边的中点.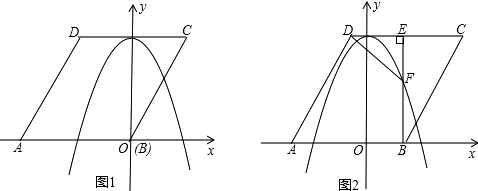
(1)求这条抛物线的函数解析式;
(2)将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移(如图2),过点B作BE⊥CD于点E,交抛物线于点F,连接DF、AF.设菱形ABCD平移的时间为t秒(0<t<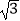 )
)
①是否存在这样的t,使△ADF与△DEF相似?若存在,求出t的值;若不存在,请说明理由;
②连接FC,以点F为旋转中心,将△FEC按顺时针方向旋转180°,得△FE′C′,当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中(包括边界)时,求t的取值范围.(写出答案即可)
相关试题

