【题目】一天,小战和同学们一起到操场测量学校旗杆高度,他们首先在斜坡底部C地测得旗杆顶部A的仰角为45°,然后上到斜坡顶部D点处再测得旗杆顶部A点仰角为37°(身高忽略不计).已知斜坡CD坡度i=1:2.4,坡长为2.6米,旗杆AB所在旗台高度EF为1.4米,旗台底部、台阶底部、操场在同一水平面上.则请问旗杆自身高度AB为( )米.
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
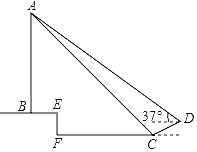
A.10.2B.9.8C.11.2D.10.8
参考答案:
【答案】B
【解析】
如图,作![]() 交
交![]() 的延长线于
的延长线于![]() ,延长
,延长![]() 交
交![]() 的延长线于
的延长线于![]() ,作
,作![]() 于
于![]() .设
.设![]() ,在
,在![]() 中,根据
中,根据![]() ,构造方程解决问题即可.
,构造方程解决问题即可.
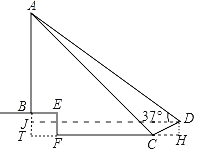
解:如图,作DH⊥FC交FC的延长线于H,延长AB交CF的延长线于T,作DJ⊥AT于J.
由题意四边形EFTB四边形DHTJ是矩形,
∴BT=EF=1.4米,JT=DH,
在Rt△DCH中,∵CD=2.6米,![]() =
=![]() ,
,
∴DH=1(米),CH=2.4(米),
∵∠ACT=45°,∠T=90°,
∴AT=TC,
设AT=TC=x.则DJ=TH=(x+2.4)米,AJ=(x﹣1)米,
在Rt△ADJ中,∵tan∠ADJ=![]() =0.75,
=0.75,
∴![]() =0.75,
=0.75,
解得x=2,
∴AB=AT﹣BT=AT﹣EF=11.2﹣1.4=9.8(米),
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离
 与小王的行驶时间
与小王的行驶时间 之间的函数关系.
之间的函数关系.请你根据图象进行探究:
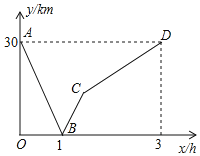
(1)小王和小李的速度分别是多少?
(2)求线段
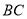 所表示的
所表示的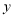 与
与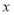 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量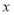 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
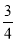 x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=
x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=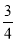 x2+bx+c经过点B,C,与x轴的另一个交点为点A.
x2+bx+c经过点B,C,与x轴的另一个交点为点A.(1)求抛物线的解析式;
(2)点P是直线BC下方的抛物线上一动点,求四边形ACPB的面积最大时点P的坐标;
(3)若点M是抛物线上一点,请直接写出使∠MBC=
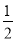 ∠ABC的点M的坐标.
∠ABC的点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线y1=﹣
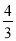 x与双曲线y=
x与双曲线y=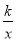 交于A,B两点,点C在x轴上,连接AC,BC.当AC⊥BC,S△ABC=15时,求k的值为( )
交于A,B两点,点C在x轴上,连接AC,BC.当AC⊥BC,S△ABC=15时,求k的值为( )
A.﹣10B.﹣9C.6D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的分式方程
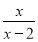 ﹣
﹣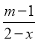 =3的解为正整数,且关于y的不等式组
=3的解为正整数,且关于y的不等式组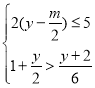 至多有六个整数解,则符合条件的所有整数m的取值之和为( )
至多有六个整数解,则符合条件的所有整数m的取值之和为( )A.1B.0C.5D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠ACB=45°,D为AC上一点,AD=5
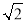 ,连接BD,将△ABD沿BD翻折至△EBD,点A的对应点E点恰好落在边BC上.延长BC至点F,连接DF,若CF=2,tan∠ABD=
,连接BD,将△ABD沿BD翻折至△EBD,点A的对应点E点恰好落在边BC上.延长BC至点F,连接DF,若CF=2,tan∠ABD=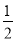 ,则DF长为( )
,则DF长为( )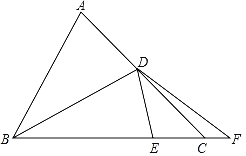
A.
 B.
B.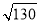 C.5
C.5 D.7
D.7
-
科目: 来源: 题型:
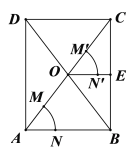
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC与BD相交于点O,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AO,AB于点M,N;②以点O为圆心,以AM长为半径作弧,交OC于点M';③以点M'为圆心,以MN长为半径作弧,在∠COB内部交前面的弧于点N';④过点N'作射线ON'交BC于点E.若AB=8,则线段OE的长为_______.
相关试题

