【题目】如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE. 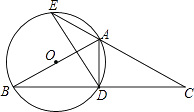
(1)求证:D是BC的中点;
(2)若DE=3,BD﹣AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
参考答案:
【答案】
(1)证明:∵AB是圆O的直径,
∴AD⊥BC,
∵AB=AC,
∴BD=DC
(2)解:∵AB=AC,
∠B=∠C,
∵∠B=∠E,
∴∠E=∠C,
∴BD=DC=DE=3,
∵BD﹣AD=2,
∴AD=1,
在RT△ABD中,AB= ![]() =
= ![]() ,
,
∴⊙O的半径为 ![]()
(3)解:∵AB=AC= ![]() ,BD=DC=3,
,BD=DC=3,
∴BC=6,
∵∠B=∠E,∠C=∠C,
∴△EDC∽△BAC,
∵ACEC=DCBC,
∴ ![]() EC=3×6,
EC=3×6,
∴EC= ![]() ,
,
∴AE=EC﹣AC= ![]() ﹣
﹣ ![]() =
= ![]()
【解析】(1)根据圆周角定理求得AD⊥BC,根据等腰三角形三线合一的性质即可证得结论;(2)先求得∠E=∠C,根据等角对等边求得BD=DC=DE=3,进而求得AD=1,然后根据勾股定理求得AB,即可求得圆的半径;(3)根据题意得到AC= ![]() ,BC=6,DC=3,然后根据割线定理即可求得EC,进而求得AE.
,BC=6,DC=3,然后根据割线定理即可求得EC,进而求得AE.
【考点精析】掌握等腰三角形的性质和圆周角定理是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某运动品牌店对第一季度A、B两款运动鞋的销售情况进行统计.两款运动鞋的销售量及总销售额如图所示:

(1)一月份B款运动鞋的销售量是A款的 ,则一月份B款运动鞋销售了多少双?
,则一月份B款运动鞋销售了多少双?
(2)第一节度这两款运动鞋的销售单价保持不变,求三月份的总销售额(销售额=销售单价×销售量);
(3)综合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议. -
科目: 来源: 题型:
查看答案和解析>>【题目】去年春季,蔬菜种植场在15公顷的大棚地里分别种植了茄子和西红柿,总费用是
 万元
万元 其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:每公顷费用
 万元
万元
每公顷获利
 万元
万元
茄子

西红柿


请解答下列问题:
 求出茄子和西红柿的种植面积各为多少公顷?
求出茄子和西红柿的种植面积各为多少公顷? 种植场在这一季共获利多少万元?
种植场在这一季共获利多少万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为
 ,C点的坐标为
,C点的坐标为 ,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着
,点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着 的路线移动
的路线移动 即:沿着长方形移动一周
即:沿着长方形移动一周 .
. 写出点B的坐标
写出点B的坐标 ______
______
 当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标.
当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标. 在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A、B的距离,飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了500米,在点D测得端点B的俯角为45°,求岛屿两端A、B的距离(结果精确到0.1米,参考数据:
 )
)
-
科目: 来源: 题型:
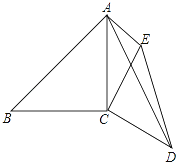
查看答案和解析>>【题目】如图,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(请在括号里注明重要的推理依据)
如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .

相关试题

