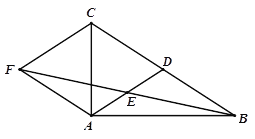
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=BD;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
参考答案:
【答案】(1)证明见解析;(2)四边形ADCF是菱形,证明见解析.
【解析】试题分析:(1)利用AAS定理判定三角形全等即可;(2)先判定四边形的形状,再根据直角三角形斜边上的中线等于斜边的一半,得出四边形是平行四边形,再加上领边相等得出菱形即可.
试题解析:
(1)证明∵AF∥BC ∴∠EFA=∠EBD∵ E是AD的中点 ∴AE=DE ∵∠FEA=∠DEB ∴ΔAEF≌ΔDEB(4分)
(2)四边形ADCF是菱形.
理由:∵CA⊥AB∴ΔACB是RtΔ,∵AD是CD边的中线
∴AD=CD=DB.由(1)知AF=DB∴AF=CD又AF∥CD∴四边形ADCF是平行四边形
又∵DA=DC∴平行四边形ADCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过A(0,3),B(2,3)两点.请你写出一组满足条件的a,b的对应值.a=____,b=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数y =
 的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标.
的图象经过点A(1,-3),一次函数y =kx +b的图象经过点A与点C(0,-4),且与反比例函数的图象相交于另一点B.试确定点B的坐标. 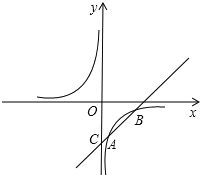
-
科目: 来源: 题型:
查看答案和解析>>【题目】国家海洋局将中国钓鱼岛最高峰命名为“高华峰”,并对钓鱼岛进行常态化立体巡航.如图1,在一次巡航过程中,巡航飞机飞行高度为2001米,在点A测得高华峰峰顶F点的俯角为30°,保持方向不变前进1200米到达B点后测得峰顶F点俯角为45°,如图2.请据此计算钓鱼岛的最高海拔高度是多少米.(结果保留整数,参考数值:
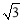 =1.732,
=1.732,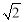 =1.414)
=1.414)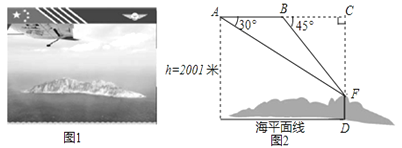
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级四个班的代表队准备举行篮球友谊赛. 甲、乙、丙三位同学预测比赛的结果如下:甲说:“902班得冠军,904班得第三”;乙说:“901班得第四,903班得亚军”;丙说:“903班得第三,904班得冠军”. 赛后得知,三人都只猜对了一半,则得冠军的是 _________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中计算结果为9的是( )
A. (﹣2)+(﹣7) B. ﹣32 C. (﹣3)2 D. 3×3﹣1
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣3的相反数是 .
相关试题

