搜索
【题目】在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A1，作第1个正方形A1B1C1C；延长C1B1交x轴于点A2，作第2个正方形A2B2C2C1，…，按这样的规律进行下去，第2016个正方形的面积是______．
参考答案：
【答案】5×（
）4030
【解析】解：如图，∵四边形ABCD是正方形，∴∠ABC=∠BAD=90°，AB=BC，
∴∠ABA1=90°，∠DAO+∠BAA1=180°﹣90°=90°，
∵∠AOD=90°，∴∠ADO+∠DAO=90°，∴∠ADO=∠BAA1，
在△AOD和A1BA中
∴△AOD∽△A1BA，
∴
，∴BC=2A1B.
∴A1C=
BC，则A2C1=
A1C，A3C2=
A2C1，
即后一个正方形的边长是前一个正方形的边长的
倍.
∴第2016个正方形的边长为
BC.
∵A的坐标为（1，0），D点坐标为（0，2），∴BC=AD=
.
∴第2011个正方形的面积为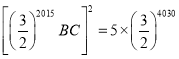
.
故答案为
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知在四边形ABCD中，点E在AD上，∠BCE=∠ACD=90°，∠BAC=∠D，BC=CE．
（1）求证：AC=CD；
（2）若AC=AE，求∠DEC的度数．
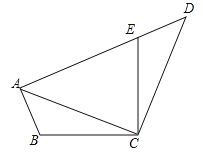
【答案】（1）证明见解析；（2）112.5°．
【解析】试题分析：
根据同角的余角相等可得到
结合条件
，再加上
可证得结论；
根据
得到
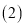根据等腰三角形的性质得到
由平角的定义得到
试题解析：
证明：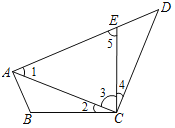
在△ABC和△DEC中，
，
（2）∵∠ACD＝90°，AC＝CD，
∴∠1＝∠D＝45°，
∵AE＝AC，
∴∠3＝∠5＝67.5°，
∴∠DEC＝180°－∠5＝112.5°．
【题型】解答题
【结束】
21【题目】一个零件的形状如图所示，工人师傅按规定做得∠B=90°，
AB＝3，BC＝4，CD＝12，AD＝13，假如这是一块钢板，你能帮工人师傅计算一下这块钢板的面积吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】向阳中学数学兴趣小组对关于x的方程（m+1）
+（m﹣2）x﹣1=0提出了下列问题：（1）是否存在m的值，使方程为一元二次方程？若存在，求出m的值，并解此方程；
（2）是否存在m的值，使方程为一元一次方程？若存在，求出m的值，并解此方程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知
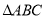中， 
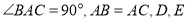是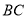
边上的点，将
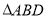绕点
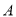旋转，得到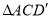
.（1）当
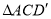时，求证：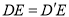 
.（2）在（1）的条件下，猜想
， 
， 
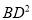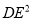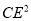有怎样的数量关系，并说明理由．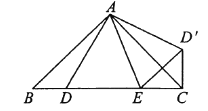
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个零件的形状如图所示，工人师傅按规定做得∠B=90°，
AB＝3，BC＝4，CD＝12，AD＝13，假如这是一块钢板，你能帮工人师傅计算一下这块钢板的面积吗？
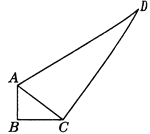
【答案】面积等于36
【解析】试题分析：利用勾股定理求AC,再利用勾股定理逆定理求∠ACB=90°，分别求
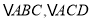的面积.试题解析：
∠B=90°，AB＝3，BC＝4,AC=
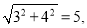
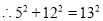=169,所以∠ACD=90°,
.所以面积是36.
【题型】解答题
【结束】
22【题目】如图，在所给正方形网格（每个小网格的边长是1）图中完成下列各题.
（1）格点△ABC（顶点均在格点上）的面积=_________；
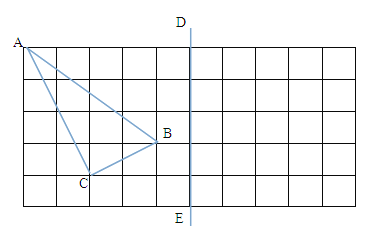
（2）画出格点△ABC关于直线DE对称的△A1B1C1；
（3）在DE上画出点P，使PB+PC最小，并求出这个最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】当m是何值时，关于x的方程（m2+2）x2+（m﹣1）x﹣4=3x2
（1）是一元二次方程；
（2）是一元一次方程；
（3）若x=﹣2是它的一个根，求m的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】解方程（组）
（1）
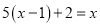
（2）
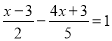
（3）
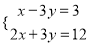
（4）
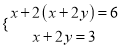
相关试题
