【题目】△ABC和△A′B′C′中,∠A=60°,∠B=40°,∠A’=60°,当∠C′= 时,△ABC∽△A′B′C′.
参考答案:
【答案】80°
【解析】∵∠A=60°,∠B=40°,
∴∠C=180°-60°-40°=80°,
∵△ABC∽△A′B′C′
∴∠C=∠C′=80°,
∴当∠C′=80°时,△ABC∽△A′B′C′.
所以答案是:80°.
【考点精析】解答此题的关键在于理解相似三角形的判定的相关知识,掌握相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AF平分∠BAC,过F作FD⊥BC,若∠B比∠C大20度,则∠F的度数是( )
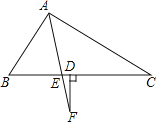
A.10°
B.15°
C.20°
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形的周长是40cm,被两条对角线分成的相邻两个三角形的周长的差是8cm,则较长的边长为____;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果函数y=x2+4x﹣m的图象与x轴有公共点,那么m的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门。乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元。
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量
 的取值范围;
的取值范围;(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 的图象的一支位于第一象限.
的图象的一支位于第一象限.(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于
 轴对称,若△OAB的面积为6,求m的值.
轴对称,若△OAB的面积为6,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁在点A(1,﹣2)向下平移5个单位长度得到点B,则点B的坐标是 .
相关试题

