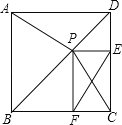
【题目】如图,P是正方形ABCD对角线BD上一点,PE⊥DC,PF⊥BC,E、F分别为垂足.
(1)求证:△APD≌△CPD;
(2)若CF=3,CE=4,求AP的长.
参考答案:
【答案】(1)证明见解析;(2)5.
【解析】试题分析:
(1)根据正方形的性质,用SAS证明△APD≌△CPD;
(2)证明四边形PEDF是矩形,用勾股定理求EF,结合矩形的性质和(1)的结论求AP的长.
试题解析:
证明:(1)∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP=45°,∠BCD=90°,
在△APD和△CPD中,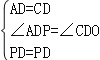 ,
,
∴△APD≌△CPD(SAS);
(2)解:∵△APD≌△CPD,∴AP=PC,
∵四边形ABCD是正方形,∴∠BCD=90°,
∵PE⊥DC,PF⊥BC,∴∠PEC=∠PFC=90°,
∴四边形PECF是矩形,∴PC=EF,∴AP=EF.
∵∠DCB=90°,∴在Rt△CEF中,EF=![]() =
=![]() =5,
=5,
∴AP=EF=5.
-
科目: 来源: 题型:
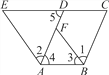
查看答案和解析>>【题目】如图,已知∠1=∠2,∠3=∠E,∠4=∠5,请判断AD与BC的位置关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,两位家长计划带领若干名学生去旅游,他们联系了报价均为每人1000元的两家旅行社.经协商,甲旅行社的优惠条件是:两位家长全额收费,学生都按7折收费;乙旅行社的优惠条件是:学生、家长都按8折收费.假设这两位家长带领x名学生去旅行,甲、乙旅行社的收费分别为y甲,y乙,
(1)写出y甲,y乙与x的函数关系式.
(2)学生人数在什么情况下,选择哪个旅行社合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应国家节能减排的号召,鼓励居民节约用电,各省先后出台了居民用电“阶梯价格”制度,如下表是某省的电价标准(每月).例如:方女士家5月份用电500度,电费=180×0.6+220×二档电价+100×三档电价=352元;李先生家5月份用电460度,交费316元.请问表中二档电价、三档电价各是多少?
阶梯
电量
电价
一档
0~180度
0.6元/度
二档
181~400度
二档电价
三档
401度及以上
三档电价
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生参加户外活动的情况,和谐中学对学生每天参加户外活动的时间进行抽样调查,并将调查结果绘制成如图两幅不完整的统计图,根据图示,请回答下列问题:
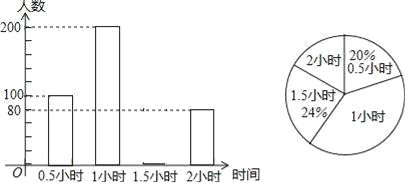
(1)求被抽样调查的学生有多少人?并补全条形统计图;
(2)该校共有1850名学生,请估计该校每天户外活动时间超过1小时的学生有多少人?
-
科目: 来源: 题型:
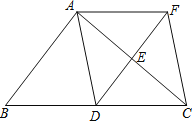
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.
(1)求证:四边形ADCF是平行四边形;
(2)当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明不小心把一块三角形形状的玻璃打碎成了三块,如图①②③,他想要到玻璃店去配一块大小形状完全一样的玻璃,你认为应带( )
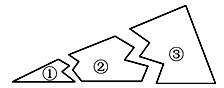
A. ① B. ② C. ③ D. ①和②
【答案】C
【解析】试题分析:根据全等三角形的判定方法带③去可以利用“角边角”得到全等的三角形.
故选C.
考点:全等三角形的应用.
【题型】单选题
【结束】
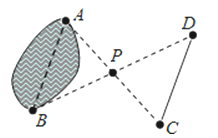
12【题目】如图,要测量池塘的宽度AB,在池塘外选取一点P,连接AP、BP并各自延长,使PC=PA,PD=PB,连接CD,测得CD长为25m,则池塘宽AB为________m,依据是________
相关试题

