【题目】如图表示一辆汽车在行驶途中的速度v(千米/时)随时间t(分)的变化示意图.
(1)从点A到点B、点E到点F、点G到点H分别表明汽车在什么状态?
(2)汽车在点A的速度是多少?在点C呢?
(3)司机在第28分钟开始匀速先行驶了4分钟,之后立即以减速行驶2分钟停止,请你在本图中补上从28分钟以后汽车速度与行驶时间的关系图.

参考答案:
【答案】(1)点A到点B是匀速运动、点E到点F是匀加速运动、点G到点H匀减速运动;(2)汽车在点A的速度是30千米每小时,在点C的速度为0千米每小时;(3)如图所示见解析.
【解析】
(1)根据图象可以确定从点A到点B、点E到点F、点G到点H分别表明汽车的运动状态;
(2)根据图象可以直接得到汽车在点A和点C的速度;
(3)结合已知条件利用图象可以画出从28分钟以后汽车速度与行驶时间的关系图.
(1)根据图象知道:
点A到点B是匀速运动、点E到点F是匀加速运动、点G到点H匀减速运动;
(2)根据图象知道:
汽车在点A的速度是30千米每小时,在点C的速度为0千米每小时;
(3)如图所示:
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明口袋中装有5个白球和6个红球,这些球除颜色外完全相同,充分搅匀后随机摸球.
(1)如果先摸出一白球,将这个白球放回,再摸出一球,那么它是白球的概率是多少?
(2)如果先摸出一白球,这个白球不放回,再摸出一球,那么它是白球的概率是多少?
(3)如果先摸出一红球,这个红球不放回,再摸出一球,那么它是白球的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,
 ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正确的序号是______.
∠AOD;③DM⊥CE;④CM+DM的最小值是10,其中正确的序号是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,直线a为对称轴,A和C都在对称轴上.
(1)△ABC以直线a为对称轴作△AB1C;
(2)若∠BAC=30°,则∠BAB1=______°;
(3)求△ABB1的面积等于______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D 的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
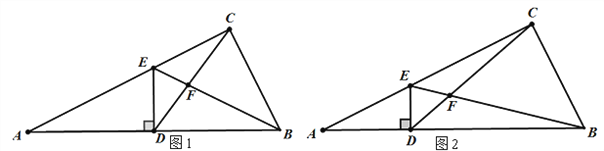
查看答案和解析>>【题目】如图1,点D为直角三角形ABC的斜边AB上的中点,DE⊥AB交AC于E, 连EB、CD,线段CD与BF交于点F.若tanA=
 ,则
,则 =_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若
=_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若 ,tanA=
,tanA= ,则
,则 =____.
=____.
相关试题

