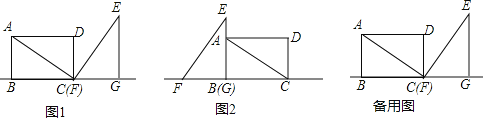
【题目】已知矩形ABCD中,AD=6,∠ACB=30°,将△ACD绕点C顺时针旋转得到△EFG,使点D的对应点G落在BC延长线上,点A对应点为E点,C点对应点为F点,F点与C点重合(如图1),此时将△EFG以每秒1个单位长度的速度沿直线CB向左平移,直至点G与点B重合时停止运动,设△EFG运动的时间为t(t>0).
(1)当t为何值时,点D落在线段EF上?
(2)设在平移过程中△EFG与矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出相应的t的取值范围;
(3)在平移过程中,当点G与点B重合时(如图2),将△CBA绕点B逆时针旋转得到△C1A1B,直线EF与C1A1所在直线交于P点,与C1B所在直线交于点Q.在旋转过程中,△ABC的旋转角为α(0°<α<180°),是否存在这样的α,使得△C1PQ为等腰三角形?若存在,请写出α的度数,若不存在,请说明理由.
参考答案:
【答案】(1)当t=2时,点D落在线段EF上.(2)见解析;(3)△C1PQ为等腰三角形,旋转角为30°、120°、165°.
【解析】
试题分析:(1)利用三角函数求出线段CD,延长AD交EF于点H,利用三角函数即可求出线段DH长度,再除以运动速度即为运动时间;
(2)分五种情况进行讨论,求出重合面积,写出S关于t的函数关系式即可;
(3)通过分析△C1PQ为等腰三角形,分析等腰情况,分别求出对应角度即可.
解:(1)∵AD=BC=6,∠ACB=30°,
∴AB=DF=6×tan30°=2![]() ,
,
延长AD交EF于点H,如下图:
∵△ACD绕点C顺时针旋转得到△EFG,
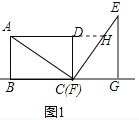
∴∠DFH=30°,
∴DH=DF×tan30°=2,
∵△EFG以每秒1个单位长度的速度沿直线CB向左平移,2÷1=2秒,
∴当t=2时,点D落在线段EF上.
(2)当0<t≤2时,S=![]() t2,
t2,
当2<t≤2![]() 时,S=2
时,S=2![]() t﹣2
t﹣2![]() ,
,
当2![]() <t≤6时,S=12﹣2
<t≤6时,S=12﹣2![]() ,
,
当6<t≤8时,S=﹣![]() t2+6
t2+6![]() t﹣20
t﹣20![]() +12,
+12,
当8<t<6+2![]() 时,S=﹣2
时,S=﹣2![]() t+12
t+12![]() +12,
+12,
(3)30°、120°、165°.
∵△C1PQ为等腰三角形,
当PQ=PC′,如下图:
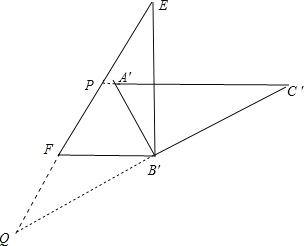
则∠Q=∠C′=30°,
∴∠EPC′=60°,
∵∠E=30°,
∴∠A′B′E=30°,
∴α=30°.
同理:当PQ=QC′,PC′=QC′,α=120°、165°.
∴△C1PQ为等腰三角形,旋转角为30°、120°、165°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)(﹣23)+(﹣12)
(2)
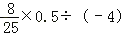
(3)1+(﹣2)+|﹣3|﹣5
(4)(﹣4)×2×(﹣0.25)
(5)
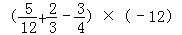
(6)
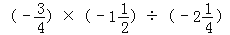
(7)(﹣
 )×42﹣0.25×(﹣8)×(﹣1)2011
)×42﹣0.25×(﹣8)×(﹣1)2011(8)﹣22﹣6÷(﹣2)×
 ﹣|﹣9+5|
﹣|﹣9+5| -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;

(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
(2)如图(2),当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形中,一个角为50°,则这个等腰三角形的顶角的度数为( )
A. 150° B. 80° C. 50°或80° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个两位数,其十位数字为a,个位数字为b,将该两位数的两个数字颠倒,得到一个新的两位数,那么这个新两位数十位上的数字与个位上的数字的和与这个新两位数的积用代数式表示为__
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将长度为a﹣2,a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,那么a的取值范围是____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( )
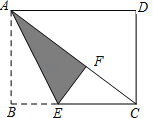
A.3 B.4 C.5 D.6
相关试题

