【题目】如图,正方形ABCD的边长为2 cm,△PMN是一块直角三角板(∠N=30°),PM>2 cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=x cm,三角板与正方形重叠部分的面积为y cm2.

下列结论:
①当0≤x≤![]() 时,y与x之间的函数关系式为y=
时,y与x之间的函数关系式为y= ![]() x2;
x2;
②当![]() 时,y与x之间的函数关系式为y=2x-
时,y与x之间的函数关系式为y=2x-![]() ;
;
③当MN经过AB的中点时,y= ![]() (cm2);
(cm2);
④存在x的值,使y= ![]() S正方形ABCD(S正方形ABCD表示正方形ABCD的面积).
S正方形ABCD(S正方形ABCD表示正方形ABCD的面积).
其中正确的是______(写出所有正确结论的序号).
参考答案:
【答案】①②④
【解析】试题分析:①在所给x的范围内,根据正切的概念求出BE,然后利用三角形面积公式可得到y与x之间的函数关系式,进而判断正误;
②在所给x的范围内,重叠图形为梯形,可利用正切定义得到梯形的底,然后根据公式求出y与x之间的函数关系式,再判断即可;
③当MN经过AB的中点时,根据BE=1,求出BM的长,即可求出y的值进行判断;
④假设存在x的值,根据题意进行解答,求出x,看是否符合条件即可.
解:如图1,

当MN经过点A时,
tan∠BAM=![]() ,
,
∴BM=AB×tan30°=2×![]() =
=![]() .
.
①如图2,

当0≤x≤![]() 时,
时,
在Rt△EBM中,tan∠EMB=![]() ,
,
∴BE=![]() x,
x,
∴y=![]() x·
x·![]() x=
x=![]() x2,故①正确;
x2,故①正确;
②如图3,

图3
当![]() ≤x≤2时,
≤x≤2时,
作EF⊥BC于F,
则EF=AB=2,FM=![]() ,
,
∴AE=BF=x-![]() ,
,
∴y=![]() ×2×
×2×![]() + (x-
+ (x-![]() )×2=2x-
)×2=2x-![]() ,故②正确;
,故②正确;
③当MN经过AB的中点时,BE=1,
则BM=![]() ,
,
∴y=![]() ×
×![]() ×1=
×1=![]() ,故③不正确;
,故③不正确;
④当y=![]() S正方形ABCD时,
S正方形ABCD时,
2x-![]() =
=![]() ×22,
×22,
解得,x=![]() ,符合题意,故④正确.
,符合题意,故④正确.
故答案为①②④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 分别与x轴、y轴交于
分别与x轴、y轴交于 两点,与直线
两点,与直线 交于点C(4,2).
交于点C(4,2).(1)点A坐标为( , ),B为( , );
(2)在线段
 上有一点E,过点E作y轴的平行线交直线
上有一点E,过点E作y轴的平行线交直线 于点F,设点E的横坐标为m,当m为何值时,四边形
于点F,设点E的横坐标为m,当m为何值时,四边形 是平行四边形;
是平行四边形;(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得
 四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
四个点能构成一个菱形.若存在,求出所有符合条件的Q点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解2014年八年级学生课外书籍借阅情况,从中随机抽取了50名学生课外书籍借阅情况,将统计结果列出如下的表格,并绘制成如图所示的扇形统计图,其中科普类册数占这50名学生借阅总册数的40%.
类别
科普类
教辅类
文艺类
其他
册数(本)
168
105
m
32
(1)表格中字母m的值等于 ;
(2)扇形统计图中“教辅类”所对应的圆心角α的度数为 °;
(3)该校2014年八年级有600名学生,请你估计该年级学生共借阅教辅类书籍约多少本?

-
科目: 来源: 题型:
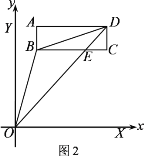
查看答案和解析>>【题目】如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6),点X,Y分别在x,y轴上.
(1)请直接写出D点的坐标 ;
(2)连接OB、OD,OD交BC于点E,∠BOY的平分线和∠BEO的平分线交于点F,若∠BOE=n,求∠OFE的度数.
(3)若长方形ABCD以每秒
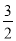 个单位的速度向下运动,设运动时间为t秒,问在第一象限内是否存在某一时刻t,使△OBD的面积等于长方形ABCD的面积的
个单位的速度向下运动,设运动时间为t秒,问在第一象限内是否存在某一时刻t,使△OBD的面积等于长方形ABCD的面积的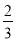 ?若存在,请求出t的值,若不存在,请说明理由。
?若存在,请求出t的值,若不存在,请说明理由。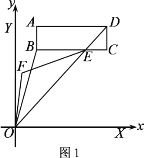
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=3,OC=2,F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=
 (x>0)的图象与BC边交于点E.
(x>0)的图象与BC边交于点E.(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=6,∠ABC=60°,M为AD中点,P为对角线BD上一动点,连接PA和PM,则PA+PM的最小值是( )

A.3B.2
 C.3
C.3 D.6
D.6
相关试题

