【题目】对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a﹣b|.
![]()
(1)计算2⊙(﹣3)的值;
(2)当a,b在数轴上的位置如图所示时,化简a⊙b;
(3)已知(a⊙a)⊙a=8+a,求a的值.
参考答案:
【答案】(1)2⊙(﹣3)=6;(2)a⊙b=﹣2b;(3)当a≥0时, a=![]() ;当a<0时, a=﹣
;当a<0时, a=﹣![]() .
.
【解析】
(1)根据文中的新运算法则将2⊙(﹣3)转化为我们熟悉的计算方式进行计算即可;
(2)根据文中的新运算法则将a⊙b转化为|a+b|+|a﹣b|,然后先判断出a+b与a﹣b的正负性,之后利用绝对值代数意义化简即可;
(3)先根据文中的新运算法则将(a⊙a)⊙a转化为我们熟悉的计算方式,此时注意对a进行分a≥0、a<0两种情况讨论,然后得出新的方程求解即可.
(1)由题意可得:2⊙(﹣3)=|2﹣3|+|2+3|=6;
(2)由数轴可知,a+b<0,a﹣b>0,
∴a⊙b=|a+b|+|a﹣b|=﹣a﹣b+a﹣b=﹣2b;
(3)当a≥0时,(a⊙a)⊙a=2a⊙a=4a=8+a,
∴a=![]() ;
;
当a<0时,(a⊙a)⊙a=(﹣2a)⊙a=﹣4a=8+a,
∴a=![]() .
.
综上所述,a的值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区30万电视观众对新闻、动画、娱乐三类节目的喜爱情况,根据老年人、成年人、青少年各年龄段实际人口的比例3:5:2,随机抽取一定数量的观众进行调查,得到如下统计图.
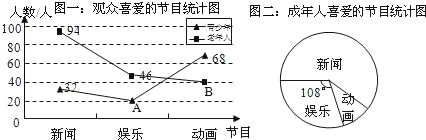
(1)上面所用的调查方法是 (填“全面调查”或“抽样调查”);
(2)写出折线统计图中A、B所代表的值和抽取观众的总人数是多少;
(3)求该地区喜爱娱乐类节目的成年人的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一病人发高烧进医院进行治疗,医生给他开了药并挂了水,同时护士每隔1小时对病人测体温,及时了解病人的好转情况,现护士对病人测体温的变化数据如下表:
时 间
7:00
8:00
9:00
10:00
11:00
12:00
13:00
14:00
15:00
体温
 (与前一次比较)
(与前一次比较)升0.2
降1.0
降0.8
降1.0
降0.6
升0.4
降0.2
降0.2
降0
注:病人早晨进院时医生测得病人体温是40.2℃。
问:(1)病人什么时候体温达到最高,最高体温是多少?
(2)病人中午12点时体温多高?
(3)病人几点后体温稳定正常?(正常体温是37℃)
-
科目: 来源: 题型:
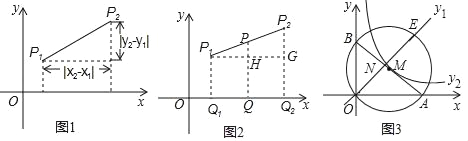
查看答案和解析>>【题目】阅读理解:数和形是数学的两个主要研究对象,我们经常运用数形结合,树形转化的方法解决一些数学问题,小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:P1P2=
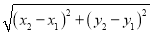 ,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=
,他还利用图2证明了线段P1P2的中点P(x,y),P的坐标公式:x=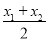 ,y=
,y=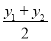 .
.启发应用:
如图3:在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A,B,
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由;
(3)若∠BOA的平分线交AB于点N,交⊙M于点E,分别求出OE的表达式y1,过点M的反比例函数的表达式y2,并根据图象,当y2>y1>0时,请直接写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小虫从某点
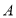 出发在一条直线上来回爬行,规定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次记为(单位:
出发在一条直线上来回爬行,规定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次记为(单位: )-11、+8、+9、-3、-6、+12、-9.
)-11、+8、+9、-3、-6、+12、-9.(1)小虫最后中否回到出发点,请判断并且通过计算说明理由.
(2)在爬行的过程中,如果每爬行一个单位长度奖励一粒芝麻,则整个运动过程中小虫一共得到多少粒芝麻?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设
 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;(3)当∠ABE的正切值是
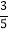 时,求AB的长.
时,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,四边形
 和
和 分别是边长为
分别是边长为 和
和 的正方形.
的正方形.
(1)用含
 和
和 的代数式表示图中三角形
的代数式表示图中三角形 的面积.
的面积.(2)用用
 和
和 的代数式表示图中阴影部分的面积.
的代数式表示图中阴影部分的面积.(3)小军计算出当
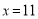 ,
, 时的阴影部分面积,与小明计算的当
时的阴影部分面积,与小明计算的当 ,
, 时的阴影部分面积相等,为什么呢?请说明理由,并求出此时的阴影部分面积.
时的阴影部分面积相等,为什么呢?请说明理由,并求出此时的阴影部分面积.
相关试题

