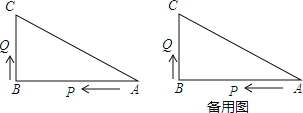
【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求△PBQ的面积;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
参考答案:
【答案】(1)S△PBQ=![]() ;(2)出发
;(2)出发![]() 秒钟后,△PQB能形成等腰三角形 ;(3)当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.
秒钟后,△PQB能形成等腰三角形 ;(3)当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.
【解析】
(1)根据点P、Q的速度求出AP、BQ的长,再求出BP的长,利用三角形面积公式计算即可;(2)设出发t秒钟后,△PQB能形成等腰三角形,则BP=BQ,由BQ=2t,BP=16-t,列式求得t即可;(3)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:①当CQ=BQ时,则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得t;②当CQ=BC时,则BC+CQ=12,易求得t;③当BC=BQ时,过B点作BE⊥AC于点E,则求出BE,CE,即可得出t.
(1)∵BQ=2×2=4(cm),AP=2×1=2cm,
BP=AB﹣AP=16﹣2=14(cm ),
∵∠B=90°,
∴S△PBQ=![]()
(2)设出发t秒钟后,△PQB能形成等腰三角形,
BQ=2t,BP=16﹣t,
根据题意得:2t=16﹣t,
解得:t =![]() ,
,
即出发![]() 秒钟后,△PQB能形成等腰三角形.
秒钟后,△PQB能形成等腰三角形.
(3)①当CQ=BQ时,如图1所示,
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ +∠ABQ=90°.
∠A +∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒.

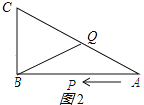
②当CQ=BC时,如图2所示,
则BC+CQ=24,
∴t=24÷2=12秒.
③当BC=BQ时,如图3所示,过B点作BE⊥AC于点E,
∵AB=16cm,BC=12cm,
∴AC=![]() =20cm.
=20cm.
则![]() ,
,
∴![]() ,
,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒.

综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,两个函数y=x,y=﹣
 x+6的图象交于点A.动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.
x+6的图象交于点A.动点P从点O开始沿OA方向以每秒1个单位的速度运动,作PQ∥x轴交直线BC于点Q,以PQ为一边向下作正方形PQMN,设它与△OAB重叠部分的面积为S.(1)求点A的坐标.
(2)试求出点P在线段OA上运动时,S与运动时间t(秒)的关系式.
(3)在(2)的条件下,S是否有最大值若有,求出t为何值时,S有最大值,并求出最大值;若没有,请说明理由.
(4)若点P经过点A后继续按原方向、原速度运动,当正方形PQMN与△OAB重叠部分面积最大时,运动时间t满足的条件是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据问题填空:
(1)计算:|﹣3|+tan60°+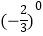 ;
;
(2)化简:(x﹣1)2+x(x+1). -
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小虎、小红三人排成一排拍照片,小明站在中间的概率是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
-
科目: 来源: 题型:
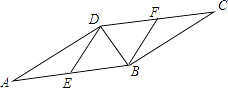
查看答案和解析>>【题目】如图,在ABCD中,BD是对角线,且DB⊥BC,E、F分别为边AB、CD的中点.求证:四边形DEBF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,M是定长线段AB上一定点,C、D两点分别从M、B出发以1cm/s、3cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)
(1)若AB=10cm,当点C、D运动了2s,求AC+MD的值.
(2)若点C、D运动时,总有MD=3AC,直接填空:AM= AB.
(3)在(2)的条件下,N是直线AB上一点,且AN-BN=MN,求
 的值.
的值.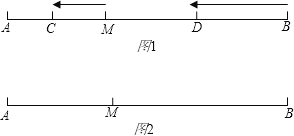
相关试题

