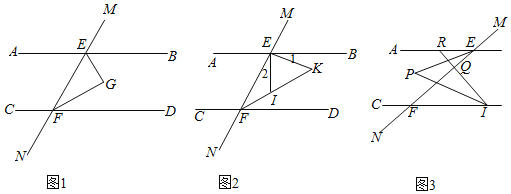
【题目】已知;直线AB∥CD,直线MN分别与AB、CD交于点E、F.
(1)如图1,∠BEF和∠EFD的平分线交于点G.求∠G的度数;
(2)如图2,EI和EK为∠BEF内满足∠1=∠2的两条线,分别与∠EFD的平分线交于点I和K,猜想∠FIE和∠K的关系,并证明;
(3)如图3,点Q为线段EF(端点除外)上的一个动点,过点Q作EF的垂线交AB于R,交CD于J,∠AEF、∠CJR的平分线相交于P,问∠EPJ的度数是否会发生变化?若不发生变化,求出∠EPJ的度数;若会发生变化,请说明理由.
参考答案:
【答案】(1)90°;(2)∠EIF+∠K=180°;(3)∠EPJ=45°;
【解析】
(1)根据![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,得到
,得到![]() ,
,![]() ,由于
,由于![]() 到
到![]() ,于是得到
,于是得到![]() ,即可得到结论;
,即可得到结论;
(2)过点![]() 作
作![]() ,由已知可得
,由已知可得![]() ,
,![]() ,得到
,得到![]() ,由于
,由于![]() 平分
平分![]() ,求得
,求得![]() ,由于
,由于![]() ,于是得到
,于是得到![]() ,由于
,由于![]() ,得到
,得到![]() ,然后根据平行线的性质即可得到结论;
,然后根据平行线的性质即可得到结论;
(3)根据![]() 、
、![]() 的平分线相交于
的平分线相交于![]() ,得到
,得到![]() ,
,![]() ,由于
,由于![]() ,得到
,得到![]() ,且
,且![]() ;根据
;根据![]() ,得
,得![]() ,再利用等量代换即可得到结论.
,再利用等量代换即可得到结论.
解:(1)∵EG、FG分别平分∠BEF和∠EFD,
∴∠BEF=2∠BEG,∠EFD=2∠GFD,
∵BE∥CF,
∴∠BEF+∠EFD=180°,
∴2∠FEG+2∠GFE=180°,
∴∠FEG+∠GFE=90°,
∵∠EGF+∠FEG+∠GFE=180°,
∴∠EGF=90°;
(2)猜想:∠EIF+∠K=180°.如图,过点I作IH∥AB,
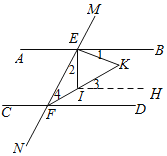
∵AB∥CD,∴IH∥CD,
由已知可得∠K=∠1+∠3,∠EIF=∠BEI+∠IFD,
∴∠3=∠KFD,
∵FK平分∠EFD,
∴∠4=∠KFD,
∵∠1=∠2,
∴∠K=∠2+∠4,
∵∠EIF=∠BEI+∠IFD,
∴∠EIF+∠K=∠2+∠4+∠BEI+∠IFD=∠BEF+∠EFD,
∵AB∥CD,
∴∠BEF+∠EFD=180°,
∴∠EIF+∠K=180°;
(3)∠EPJ=45°,理由如下:
∵AB∥CD,
∴易得∠EPJ=∠AEP+∠PIC,且∠AEF=∠JFE,
∵∠AEF、∠CJR的平分线相交于P,
∴∠AEF=2∠AEP,∠CJR=2∠PJC,
∵RJ⊥EF,
∴∠FQJ=90°,
∴∠EFJ+∠CJR=90°,
∴∠AEF+∠CJR=90°,
∴2∠AEP+2∠PJC=90°,
∴∠AEP+∠PJC=45°,
∴∠EPJ=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.
(1)如图1,若CE=CF,求证:DE=DF;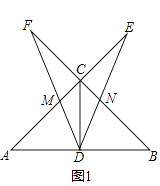
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.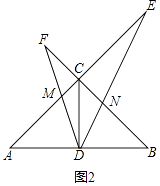
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由;
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3 时,求线段DH的长.
时,求线段DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
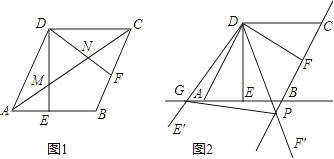
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN= AC;
AC;
(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3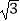 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向. -
科目: 来源: 题型:
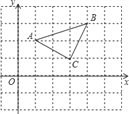
查看答案和解析>>【题目】如图所示,三角形ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).
(1)三角形A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,O是AC、BD的交点,过点O 与AC垂直的直线交边AD于点E,若□ABCD的周长为22cm,则△CDE的周长为( ).

A. 8cm B. 10cm C. 11cm D. 12cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,
, 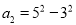 ,……,
,……,  ,(n为正整数)
,(n为正整数)(1)试说明
 是8的倍数;
是8的倍数;(2)若△ABC的三条边长分别为
 、
、 、
、 (
( 为正整数)
为正整数)①求
 的取值范围.
的取值范围.②是否存在这样的
 ,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
,使得△ABC的周长为一个完全平方数,若存在,试举出一例,若不存在,说明理由.
相关试题

