【题目】如图,AB=AE,∠B=∠E,BC=ED,点F是CD的中点,

(1)AC与AD相等吗?为什么?
(2)AF与CD的位置关系如何?说明理由;
(3)若P为AF上的一点,那么PC与PD相等吗?为什么?
参考答案:
【答案】(1)AC=AD,见解析;(2)AF⊥CD,见解析;(3)PC=PD,见解析.
【解析】
(1)由已知条件:AB=AE,∠B=∠E,BC=ED,可证得△ABC∽△AED,由此得AC=AD.
(2)由于△ACD是等腰三角形,根据等腰三角形三线合一的性质即可得到AF⊥CD.
(3)由(2)易知:AF垂直平分线段CD,即可根据线段垂直平分线的性质判定PC=PD.
(1)AC=AD.理由如下:
在△ABC与△AED中

∴△ABC≌△AED(SAS)
∴AC=AD
(2)AF⊥CD,理由如下:
∵AC=AD,点F是CD的中点
∴AF⊥CD
(3)PC=PD,理由如下:
∵点F是CD的中点,AF⊥CD
∴AF是CD的垂直平分线
∵点P在AF上
∴PC=PD

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:AB=CD;
(2)若AB=CF,∠B=30°,求∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在中
 ,
, ,
, ,
, 是
是 的平分线,交
的平分线,交 于点
于点 ,
, 是
是 的中点,连接
的中点,连接 并延长交
并延长交 的延长线于点
的延长线于点 ,连接
,连接 .
.求证:(1)
 ;
;(2)
 为等腰三角形
为等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从
 地出发,匀速驶向
地出发,匀速驶向 地.甲车以
地.甲车以 的速度行驶
的速度行驶 后,乙车沿相同的路线出发.乙车先到达
后,乙车沿相同的路线出发.乙车先到达 地并停留
地并停留 后,再以原来的速度按原路线返回,直到与甲车相遇.在这个过程中,两车之间的距离
后,再以原来的速度按原路线返回,直到与甲车相遇.在这个过程中,两车之间的距离 与乙车行驶的时间
与乙车行驶的时间 之间的函数关系如图所示,则当两车相距
之间的函数关系如图所示,则当两车相距 时,乙车出发的时间为______
时,乙车出发的时间为______ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=
 S△BOC,求点D的坐标.
S△BOC,求点D的坐标.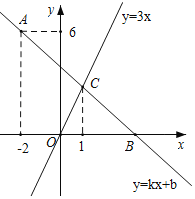
-
科目: 来源: 题型:
查看答案和解析>>【题目】某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.
设小明计划今年夏季游泳次数为x(x为正整数).
(I)根据题意,填写下表:
游泳次数
10
15
20
…
x
方式一的总费用(元)
150
175
______
…
______
方式二的总费用(元)
90
135
______
…
______
(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?
(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
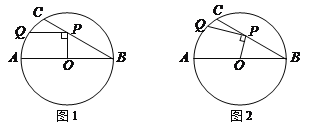
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
相关试题

