【题目】某自行车厂一周内计划平均每天生产200辆自行车,由于种种原因,实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产记为正,减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减产量/辆 |
|
|
|
|
|
|
|
(1)根据记录的数据可知,该厂星期五生产自行车 辆.
(2)根据上表记录的数据可知,该厂本周实际生产自行车 辆.
(3)该厂实行每日计件工资制,每生产一辆自行车可得60元,若超额完成任务,则超过部分每辆另外奖励15元,若完不成每天的计划量,则少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?
(4)若该厂实行每周计件工资制,每生产一辆自行车可得60元,若超额完成周计划工作量,则超过部分每辆另外奖励15元,若完不成每周的计划量,则少生产一辆扣20元,那么该厂工人这一周的工资总额是多少元?
参考答案:
【答案】(1) 190;(2) 1409;(3) 84550 元;(4) 84675元.
【解析】
(1)根据题意和表格中的数据,可以得到该厂星期五生产自行车的数量;
(2)根据题意和表格中的数据,可以得到该厂本周实际生产自行车的数量;
(3)根据题意和表格中的数据可以解答本题;
(4)根据题意和表格中的数据可以解答本题.
解:(1)∵超产记为正、减产记为负,
∴星期五生产自行车![]() (辆),
(辆),
故答案为:190;
(2)该厂本周实际生产自行车:
![]() (辆),
(辆),
故答案为:1409;
(3)![]() (辆),
(辆),
![]() (元),
(元),
答:该厂工人这一周的工资总额是84550 元;
(4)实行每周计件工资制的工资为![]() (元),
(元),
答:该厂工人这一周的工资总额是84675元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:阅读下列材料:已知二次三项式2x2+x+a有一个因式是(x+2),求另一个因式以及a 的值
解:设另一个因式是(2x+b),
根据题意,得2x2+x+a=(x+2)(2x+b),
展开,得2x2+x+a =2x2+(b+4)x+2b,
所以
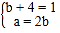 ,解得
,解得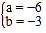 ,
,所以,另一个因式是(2x3),a 的值是6.
请你仿照以上做法解答下题:已知二次三项式3x2 10x m 有一个因式是(x+4),求另一个因式以及m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司随机选取40名员工进行普法知识考查,对考查成绩进行统计(成绩均为整数,满分100分),并依据统计数据绘制了如下尚不完整的统计表.解答下列问题:
(1) 表中a=__________,b=__________,c=__________
(2) 请补全频数分布直方图;
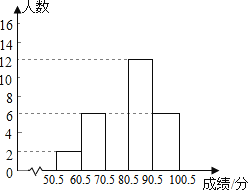
组别
分数段/分
频数/人数
频率
1
50.5~60.5
2
a
2
60.5~70.5
6
0.15
3
70.5~80.5
b
c
4
80.5~90.5
12
0.30
5
90.5~100.5
6
0.15
合计
40
1.00
(3) 该公司共有员工3000人,若考查成绩80分以上(不含80分)为优秀,试估计该公司员工“六五”普法知识知晓程度达到优秀的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,矩形 OABC 的 顶 点 A(0,3),C(- 1,0). 将 矩 形 OABC 绕原点顺时针旋转 900,得到矩形 OA’B’C’.解答下列问题:
(1)求出直线 BB’的函数解析式;
(2)直线 BB’与 x 轴交于点 M、与 y 轴交于点N,抛物线 y = ax2+ bx + c 的图象经过点C、M、N,求抛物线的函数解析式.
(3)将△MON 沿直线 MN 翻折,点 O 落在点P 处,请你判断点 P 是否在抛物线上,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2011广西崇左,18,3分)已知:二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论中:①abc>0;②2a+b<0;③a+b<m(am+b)(m≠1的实数);④(a+c)2<b2;⑤a>1.其中正确的项是( )

A. ①⑤ B. ①②⑤ C. ②⑤ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的坐标分别为A(﹣3,5),B(﹣4,2),C(﹣1,4)(注:每个方格的边长均为1个单位长度).
(1)将△ABC沿着水平方向向右平移6个单位得△A1B1C1,请画出△A1B1C1;
(2)作出将△ABC关于O点成中心对称的△A2B2C2,并直接写出的坐标;
(3)△A1B1C1与△A2B2C2是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
相关试题

