搜索
【题目】某书店为了迎接“读书节”制定了活动计划，陈经理查看计划书发现：A类图书的标价是B类图书标价的1.5倍，若顾客用1080元购买图书，能单独购买A类图书的数量恰好比单独购买B类图书的数量少20本.请求出A、B两类图书的标价.
【答案】A：27元、 B:18元
【解析】试题分析：设B类图书的标价是x元，则A类图书的标价是1.5x元，根据用1080元购买图书，单独购买A类图书的数量恰好比单独购买B类图书的数量少20本列出分式方程求解即可．
试题解析：
解：设B类图书的标价是x元，则A类图书的标价是1.5x元，
根据题意得： 
，
去分母得：1620－1080＝30x，
解得：x＝18，
经检验x＝18是原分式方程的解，
1.5x＝27，
答：A、B两类图书的标价分别为27元、18元．
【题型】解答题
【结束】
25
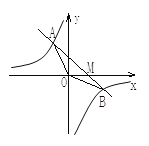
【题目】如图,已知一次函数y1=kx+b的图象与反比例函数
的图象交于A、B两点, 且点A的坐标为（-2,3），点B的纵坐标是-2,求:
(1)一次函数与反比例函数的解析式;
（2）利用图像指出，当
为何值时有
>
；当
为何值时有
＜
（3）利用图像指出，当
>3时
的取值范围。
参考答案：
【答案】见解析
【解析】试题分析：（1）把A点坐标代入反比例函数解析式求出m的值，把B点的纵坐标代入反比例函数解析式求出B点的横坐标，再把A、B两点的坐标代入一次函数解析式求出k、b的值即可；
（2）根据A、B的横坐标，结合图象即可得出答案；
（3）求出x＝3时y2的值，然后结合图象即可得出y2的取值范围．
试题解析：
解：（1）∵A（－2，3）在反比例函数y2＝
的图象上，
∴m＝－2×3
＝－6，
即反比例函数的解析式为y2＝
．
当y2＝－2时，x＝3，
即B（3，－2），
把A（－2，3），B（3，－2）代入y＝kx＋b得：
，
解得： 
，
即一次函数的解析式为y＝－x＋1；
（2）结合图象可得y1＞y2时对应的图象在点A的左侧和y轴与点B之间，
即x＜－2或0＜x＜3；
同理y1＜y2时对应的图象在点A与y轴之间和点B的右侧，
即－2＜x＜0或x＞3；
（3）当x＝3时，y2＝－2，
当x＞3时反比例函数对应的图象在点B的右侧部分，
对应的函数值－2＜y2＜0．
-
科目： 来源： 题型：
查看答案和解析>>【题目】海静中学开展以“我最喜爱的职业”为主题的调查活动，围绕“在演员、教师、医生、律师、公务员共五类职业中，你最喜爱哪一类？（必选且只选一类）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的统计图，请你根据图中提供的信息回答下列问题：
（1）本次调查共抽取了多少名学生？
（2）求在被调查的学生中，最喜爱教师职业的人数，并补全条形统计图；
（3）若海静中学共有1500名学生，请你估计该中学最喜爱律师职业的学生有多少名？
-
科目： 来源： 题型：
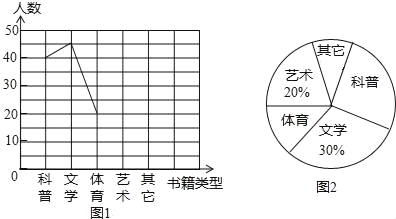
查看答案和解析>>【题目】2016年3月，某中学以“每天阅读l小时”为主题，对学生最喜爱的书籍类型进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图1和图2提供的信息，解答下列问题：
（1）请把折线统计图（图1）补充完整；
（2）如果这所中学共有学生900名，那么请你估算最喜爱科普类书籍的学生人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校男子足球队的年龄分布如图所示，则根据图中信息可知这些队员年龄的平均数，中位数分别是（ ）
A.15.5，15.5
B.15.5，15
C.15，15.5
D.15，15 -
科目： 来源： 题型：
查看答案和解析>>【题目】为了强化司机的交通安全意识，我市利用交通安全宣传月对司机进行了交通安全知识问卷调查．关于酒驾设计了如下调查问卷：
克服酒驾﹣﹣你认为哪种方式最好？（单选）
A加大宣传力度，增强司机的守法意识． B在汽车上张贴温馨提示：“请勿酒驾”．
C司机上岗前签“拒接酒驾”保证书． D加大检查力度，严厉打击酒驾．
E查出酒驾追究一同就餐人的连带责任．
随机抽取部分问卷，整理并制作了如下统计图：
根据上述信息，解答下列问题：
（1）本次调查的样本容量是多少？
（2）补全条形图，并计算B选项所对应扇形圆心角的度数；
（3）若我市有3000名司机参与本次活动，则支持D选项的司机大约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,已知一次函数y1=kx+b的图象与反比例函数
的图象交于A、B两点, 且点A的坐标为（-2,3），点B的纵坐标是-2,求:(1)一次函数与反比例函数的解析式;
（2）利用图像指出，当
为何值时有
>
；当
为何值时有
＜
（3）利用图像指出，当
>3时
的取值范围。
【答案】见解析
【解析】试题分析：（1）把A点坐标代入反比例函数解析式求出m的值，把B点的纵坐标代入反比例函数解析式求出B点的横坐标，再把A、B两点的坐标代入一次函数解析式求出k、b的值即可；
（2）根据A、B的横坐标，结合图象即可得出答案；
（3）求出x＝3时y2的值，然后结合图象即可得出y2的取值范围．
试题解析：
解：（1）∵A（－2，3）在反比例函数y2＝
的图象上，∴m＝－2×3
＝－6，
即反比例函数的解析式为y2＝
．当y2＝－2时，x＝3，
即B（3，－2），
把A（－2，3），B（3，－2）代入y＝kx＋b得：
，解得：
，即一次函数的解析式为y＝－x＋1；
（2）结合图象可得y1＞y2时对应的图象在点A的左侧和y轴与点B之间，
即x＜－2或0＜x＜3；
同理y1＜y2时对应的图象在点A与y轴之间和点B的右侧，
即－2＜x＜0或x＞3；
（3）当x＝3时，y2＝－2，
当x＞3时反比例函数对应的图象在点B的右侧部分，
对应的函数值－2＜y2＜0．
点睛：本题考查了一次函数与反比例函数的交点问题，用待定系数法求一次函数的解析式等知识点，主要考查学生的计算能力和观察图形的能力，用了数形结合思想．
【题型】解答题
【结束】
26【题目】如图，四边形ABCD是平行四边形，点A(1，0)，B(4，1)，C(4，4)．反比例函数
(x＞0)的图像经过点D，点P是一次函数y=ax+4-4a(a
0)的图像与该反比例函数图像的一个公共点． (1)求反比例函数的表达式；
(2)一次函数y=ax+4-4a(a
0)的图像恒过一定点，直接写出这个定点的坐标.(3)对于一次函数y=ax+4-4a(a
0)，当y随x的增大而减小时，确定点P的横坐标的取值范围．(不必写出过程)
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知A(－4，n)、B(3，4)是一次函数y1＝kx＋b的图象与反比例函数
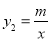的图象的两个交点，过点D(t，0)（0＜t＜3）作x轴的垂线，分别交双曲线
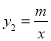和直线y1＝kx＋b于P、Q两点(1) 直接写出反比例函数和一次函数的解析式
(2) 当t为何值时，S△BPQ＝
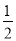S△APQ(3) 以PQ为边在直线PQ的右侧作正方形PQMN，试说明：边QM与双曲线
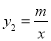（x＞0）始终有交点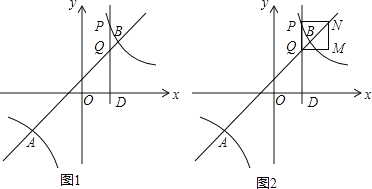
相关试题
