【题目】下列命题中,真命题是( )
A. 四个角相等的菱形是正方形 B. 对角线垂直的四边形是菱形
C. 有两边相等的平行四边形是菱形 D. 两条对角线相等的四边形是矩形
参考答案:
【答案】A
【解析】分析:根据菱形的判断方法、正方形的判断方法和矩形的判断方法逐项分析即可.
详解:
A选项:
∵四个角相等的菱形,
∴四个角为直角的菱形,即为正方形,故是真命题;
B选项:对角线垂直的四边形可能是梯形,故对角线垂直的四边形是菱形是假命题;
C选项:当相等的边是对边时,它不是菱形,故有两边相等的平行四边形是菱形是假命题;
D选项:两条对角线相等的四边形可能是等腰梯形,故两条对角线相等的四边形是矩形是假命题;
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店为了促销一种定价为3元的商品,采取下列方式优惠销售:若一次性购买不超过5件,按原价付款;若一次性购买5件以上,超过部分按原价八折付款.如果小明有30元钱,那么他最多可以购买该商品( )
A. 9件 B. 10件 C. 11件 D. 12件
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,正比例函数y=kx(k>0)与反比例函数y=
 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m , 0).其中m>0.
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为(m , 0).其中m>0.
(1)四边形ABCD的是 . (填写四边形ABCD的形状)
(2)当点A的坐标为(n,3)时,四边形ABCD是矩形,求mn的值.
(3)试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,“中国海监50”正在南海海域A处巡逻,岛礁B上的中国海军发现点A在点B的正西方向上,岛礁C上的中国海军发现点A在点C的南偏东30°方向上,已知点C在点B的北偏西60°方向上,且B、C两地相距120海里.
(1)求出此时点A到岛礁C的距离;
(2)若“中海监50”从A处沿AC方向向岛礁C驶去,当到达点A′时,测得点B在A′的南偏东75°的方向上,求此时“中国海监50”的航行距离.(注:结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BO,CO分别是∠ABC,∠ACB的平分线,∠A=50°,则∠BOC等于( )
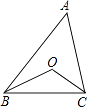
A.110°
B.115°
C.120°
D.130° -
科目: 来源: 题型:
查看答案和解析>>【题目】为了打造区域中心城市,实现攀枝花跨越式发展,我市花城新区建设正按投资计划有序推进.花城新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3 , 现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如下表所示:
租金(单位:元/台时)
挖掘土石方量(单位:m3/台时)
甲型挖掘机
100
60
乙型挖掘机
120
80
(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有哪几种不同的租用方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】平行四边形ABCD的两个顶点A、C在反比例函数
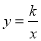 (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)若△APO的面积为2,求点D到直线AC的距离.

相关试题

