【题目】如图,四边形ABCD中,∠ABC+∠D=180°,AC平分∠BAD,CE⊥AB,CF⊥AD.试说明:
(1)△CBE≌△CDF;
(2)AB+DF=AF.

参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据角平分线的性质可得到CE=CF,根据余角的性质可得到∠EBC=∠D,已知CE⊥AB,CF⊥AD,从而利用AAS即可判定△CBE≌△CDF.
(2)已知EC=CF,AC=AC,则根据HL判定△ACE≌△ACF得AE=AF,最后证得AB+DF=AF即可.
试题解析:证明:(1)∵AC平分∠BAD,CE⊥AB,CF⊥AD
∴CE=CF
∵∠ABC+∠D=180°,∠ABC+∠EBC=180°
∴∠EBC=∠D
在△CBE与△CDF中,
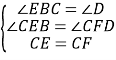 ,
,
∴△CBE≌△CDF;
(2)在Rt△ACE与Rt△ACF中,
![]()
∴△ACE≌△ACF
∴AE=AF
∴AB+DF=AB+BE=AE=AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填在相应的括号内.
-
 ,0,0.16,3
,0,0.16,3 ,
,  ,-
,- ,
,  ,
, ,-
,- ,-3.14
,-3.14有理数:{____________________________________________________};
无理数:{____________________________________________________};
负实数:{____________________________________________________}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,若S△DEC=3,则S△BCF= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接0B,OC,若△ADE的周长为6cm,△OBC的周长为16cm.
(1)求线段BC的长;
(2)连接OA,求线段OA的长;
(3)若∠BAC=120°,求∠DAE的度数.

-
科目: 来源: 题型:
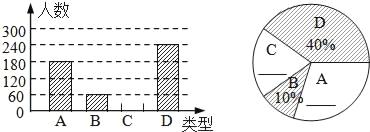
查看答案和解析>>【题目】“春节”是我国的传统佳节,民间历来有吃“汤圆”的习俗.某食品厂为了解市民对去年销量较好的肉馅(A)、豆沙馅 (B)、菜馅(C)、三丁馅 (D)四种不同口味汤圆的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).请根据以上信息回答:
(1)本次参加抽样调查的居民人数是 人;
(2)将图 ①②补充完整;( 直接补填在图中)
(3)求图②中表示“A”的圆心角的度数;
(4)若居民区有8000人,请估计爱吃D汤圆的人数.
-
科目: 来源: 题型:
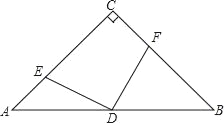
查看答案和解析>>【题目】已知:如图,在△ABC中,∠ACB=90°,AC=BC,D是AB的中点,点E在AC上,点F在BC上,且AE=CF.
(1)求证:DE=DF,DE⊥DF;
(2)若AC=2,求四边形DECF面积.
相关试题

