【题目】在图“书香八桂，阅读圆梦”读数活动中，某中学设置了书法、国学、诵读、演讲、征文四个比赛项目如图，在Rt△ABC中，∠C=90°，BD是角平分线，点O在AB上，以点O为圆心，OB为半径的圆经过点D，交BC于点E．

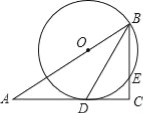
（1）求证：AC是⊙O的切线；

（2）若OB=10，CD=8，求BE的长．

参考答案：

【答案】（1）证明过程见解析；（2）12.

【解析】

试题分析：（1）连接OD，由BD为角平分线得到一对角相等，根据OB=OD，等边对等角得到一对角相等，等量代换得到一对内错角相等，进而确定出OD与BC平行，利用两直线平行同位角相等得到∠ODA为直径，即可得证；（2）由OD与BC平行得到三角形OAD与三角形BAC相似，由相似得比例求出OA的长，进而确定出AB的长，连接EF，过O作OG垂直于BC，利用勾股定理求出BG的长，由BG+GC求出BC的长，再由三角形BEF与三角形BAC相似，由相似得比例求出BE的长即可．

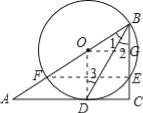
试题解析：（1）连接OD， ∵BD为∠ABC平分线， ∴∠1=∠2， ∵OB=OD， ∴∠1=∠3， ∴∠2=∠3，

∴OD∥BC， ∵∠C=90°， ∴∠ODA=90°， 则AC为圆O的切线；

（2）过O作OG⊥BC， ∴四边形ODCG为矩形， ∴GC=OD=OB=10，OG=CD=8，

在Rt△OBG中，利用勾股定理得：BG=6， ∴BC=BG+GC=6+10=16， ∵OD∥BC，

∴△AOD∽△ABC， ∴=，即=， 解得：OA=， ∴AB=+10=，

连接EF， ∵BF为圆的直径， ∴∠BEF=90°， ∴∠BEF=∠C=90°， ∴EF∥AC，

∴=，即=， 解得：BE=12．

关闭