【题目】完成下面的证明.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.
证明:∵∠1=∠2(已知),∠1=∠3,∠2=∠4 ()
∴∠3=∠4(等量代换).
∴∥()
∴∠C=∠ABD ()
∵∠C=∠D ()
∴∠D=∠ABD ()
∴AC∥DF ()
参考答案:
【答案】对顶角相等;DB;CE;内错角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行
【解析】解:∵∠1=∠2(已知),∠1=∠3,∠2=∠4 ( )
∴∠3=∠4(等量代换).
∴DB∥CE( 内错角相等,两直线平行 )
∴∠C=∠ABD ( 两直线平行,同位角相等 )
∵∠C=∠D ( 已知 )
∴∠D=∠ABD ( 等量代换 )
∴AC∥DF ( 内错角相等,两直线平行 )
故答案是:对顶角相等;DB;CE;内错角相等,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行.
【考点精析】利用平行线的判定与性质对题目进行判断即可得到答案,需要熟知由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
(1) 取点M(1,0),则点M到直线l:
 的距离为_________,取直线
的距离为_________,取直线 与直线l平行,则两直线距离为_________.
与直线l平行,则两直线距离为_________.(2) 已知点P为抛物线y=x2-4x的x轴上方一点,且点P到直线l:
 的距离为
的距离为 ,求点P的坐标.
,求点P的坐标.(3) 若直线y=kx+m与抛物线y=x2-4x相交于x轴上方两点A、B(A在B的左边),且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离的最大时直线y=kx+m的解析式.


-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2﹣ax+9是一个完全平方式,则a= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知(b+2)xb+1<-3是关于x的一元一次不等式,试求b的值,并解这个一元一次不等式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,坡面CD的坡比为
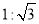 ,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是
,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC是3米,斜坡上的树影CD是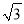 米,则小树AB的高是 米.
米,则小树AB的高是 米.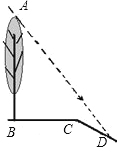
-
科目: 来源: 题型:
查看答案和解析>>【题目】4的平方根等于_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题9分)如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE
(2)若△BEF也与△ABF相似,请求出
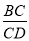 的值 .
的值 .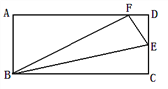
相关试题

