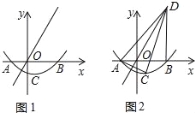
【题目】如图1,二次函数y=a(x2﹣x﹣6)(a≠0)的图象过点C(1,﹣![]() ),与x轴交于A,B两点(点A在x轴的负半轴上),且A,C两点关于正比例函数y=kx(k≠0)的图象对称.
),与x轴交于A,B两点(点A在x轴的负半轴上),且A,C两点关于正比例函数y=kx(k≠0)的图象对称.
(1)求二次函数与正比例函数的解析式;
(2)如图2,过点B作BD⊥x轴交正比例函数图象于点D,连接AC,交正比例函数的图象于点E,连接AD,CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动,当其中一个点到达终点时,另一个点随之停止运动,连接PQ,QE,PE,设运动时间为t秒,是否存在某一刻,使PE,QE分别平分∠APQ和∠PQC?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】(1)正比例函数解析式为y=![]() x.(2)见试题解析
x.(2)见试题解析
【解析】
试题分析:(1)利用待定系数法求出a的值,求出AC中点E坐标,再证明OA=OC,直线OE就是所求的正比例函数.
(2)如答图1所示,关键是证明△APE∽△CEQ.根据∠DAC=∠DCA,∠AEP=∠CQE,证明△APE∽△CEQ,根据相似线段比例关系列出方程,解方程求出时间t的值.
试题解析:(1)把点C(1,﹣![]() )代入抛物线解析式y=a(x2﹣x﹣6)得a=
)代入抛物线解析式y=a(x2﹣x﹣6)得a=![]() ,
,
∴抛物线解析式为y=![]() x2﹣
x2﹣![]() ﹣
﹣![]() ,∵OA=2,OC=
,∵OA=2,OC=![]() =2,∴OA=OC,
=2,∴OA=OC,
∵A、C中点E的坐标为(﹣![]() ,﹣
,﹣![]() ),∴直线OE垂直平分AC,即A、C关于直线OE对称,
),∴直线OE垂直平分AC,即A、C关于直线OE对称,
∴直线OE解析式为y=![]() x,∴所求是正比例函数解析式为y=
x,∴所求是正比例函数解析式为y=![]() x.
x.
(2)假设存在.
如答图1所示,在Rt△ACK中,由勾股定理得:AC=![]() =
=![]() =2
=2![]() ,∵OB=3,∴BD=3
,∵OB=3,∴BD=3![]() ,AB=OA+OB=5,在Rt△ABD中,由勾股定理得:AD=
,AB=OA+OB=5,在Rt△ABD中,由勾股定理得:AD=![]() =
=![]() =2
=2![]() ,
,
∵点A、C关于y=![]() x对称,∴CD=AD=2
x对称,∴CD=AD=2![]() ,∠DAC=∠DCA,AE=CE=
,∠DAC=∠DCA,AE=CE=![]() AC=
AC=![]() ,
,
连接PQ、PE,QE,则∠APE=∠QPE,∠PQE=∠CQE,在四边形APQC中,∠DAC+∠APQ+∠PQC+∠DCA=360°(四边形内角和等于360°),即2∠DAC+2∠APE+2∠CQE=360°,
∴∠DAC+∠APE+∠CQE=180°,又∵∠DAC+∠APE+∠AEP=180°(三角形内角和定理),
∴∠AEP=∠CQE,在△APE与△CEQ中,∵∠DAC=∠DCA,∠AEP=∠CQE,
∴△APE∽△CEQ,∴![]() =
=![]() ,即:
,即:![]() =
=![]() ,
,
整理得:2t2﹣4![]() t+3=0,
t+3=0,
解得:t=![]() 或t=
或t=![]() (t<
(t<![]() ,所以舍去),
,所以舍去),
∴存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC,此时t=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式-2x3y3+3x2y2-6xy+2的次数是____,其中二次项系数是____,按字母x的升幂排列为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解学生的课外阅读情况,随机抽取了一个班级的学生,对他们一周的读书时间进行了统计,统计数据如下表所示:
学生人数
6
10
9
8
7
读书时间(小
时)
7
8
9
10
11
则该班学生一周读书时间的中位数和众数分别是( )
A. 9,8 B. 9,9 C. 9.5,9 D. 9.5,8
-
科目: 来源: 题型:
查看答案和解析>>【题目】2的相反数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣1﹣2×(﹣2)2的结果等于___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从正多边形的一个顶点可以引出5条对角线,则这个正多边形每个外角的度数为( )
A.135°B.45°C.60°D.120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程2x+a+5=0的解是x=1,则a的值为______.
相关试题

