搜索
【题目】某校为了解学生的课外阅读情况，随机抽取了一个班级的学生，对他们一周的读书时间进行了统计，统计数据如下表所示：
学生人数 | 6 | 10 | 9 | 8 | 7 |
读书时间（小 时） | 7 | 8 | 9 | 10 | 11 |
则该班学生一周读书时间的中位数和众数分别是（ ）
A. 9，8 B. 9，9 C. 9.5，9 D. 9.5，8
参考答案：
【答案】A
【解析】
根据表格中的数据可知该班有学生 40 人，从而可以求得中位数和众数，本题得以解决．
由表格可得，
该班学生一周读书时间的中位数和众数分别是：9、8.
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果单项式-2x2ymz2的次数与单项式3.5a4b3的次数相同,则m=____.
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列计算正确的是（ ）
A. （a﹣b）2＝a2﹣b2 B. x6÷x2＝x3
C. 5a2b﹣2a2b＝3 D. （2x2）3＝8x6
-
科目： 来源： 题型：
查看答案和解析>>【题目】多项式-2x3y3+3x2y2-6xy+2的次数是____,其中二次项系数是____,按字母x的升幂排列为________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】2的相反数是______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，二次函数y=a（x2﹣x﹣6）（a≠0）的图象过点C（1，﹣
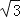），与x轴交于A，B两点（点A在x轴的负半轴上），且A，C两点关于正比例函数y=kx（k≠0）的图象对称．（1）求二次函数与正比例函数的解析式；
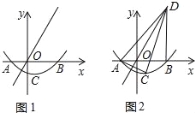
（2）如图2，过点B作BD⊥x轴交正比例函数图象于点D，连接AC，交正比例函数的图象于点E，连接AD，CD．如果动点P从点A沿线段AD方向以每秒2个单位的速度向D运动，同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动，当其中一个点到达终点时，另一个点随之停止运动，连接PQ，QE，PE，设运动时间为t秒，是否存在某一刻，使PE，QE分别平分∠APQ和∠PQC？若存在，求出t的值；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】﹣1﹣2×（﹣2）2的结果等于___________.
相关试题
