【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 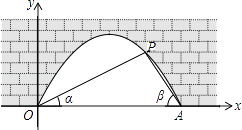
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
参考答案:
【答案】
(1)解:过点P作PH⊥OA于H,如图.
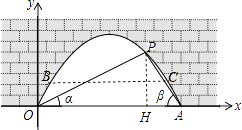
设PH=3x,
在Rt△OHP中,
∵tanα= ![]() =
= ![]() ,
,
∴OH=6x.
在Rt△AHP中,
∵tanβ= ![]() =
= ![]() ,
,
∴AH=2x,
∴OA=OH+AH=8x=4,
∴x= ![]() ,
,
∴OH=3,PH= ![]() ,
,
∴点P的坐标为(3, ![]() )
)
(2)解:若水面上升1m后到达BC位置,如图,

过点O(0,0),A(4,0)的抛物线的解析式可设为y=ax(x﹣4),
∵P(3, ![]() )在抛物线y=ax(x﹣4)上,
)在抛物线y=ax(x﹣4)上,
∴3a(3﹣4)= ![]() ,
,
解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x(x﹣4).
x(x﹣4).
当y=1时,﹣ ![]() x(x﹣4)=1,
x(x﹣4)=1,
解得x1=2+ ![]() ,x2=2﹣
,x2=2﹣ ![]() ,
,
∴BC=(2+ ![]() )﹣(2﹣
)﹣(2﹣ ![]() )=2
)=2 ![]() =2×1.41=2.82≈2.8.
=2×1.41=2.82≈2.8.
答:水面上升1m,水面宽约为2.8米
【解析】(1)过点P作PH⊥OA于H,如图,设PH=3x,运用三角函数可得OH=6x,AH=2x,根据条件OA=4可求出x,即可得到点P的坐标;(2)若水面上升1m后到达BC位置,如图,运用待定系数法可求出抛物线的解析式,然后求出y=1时x的值,就可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE.

(1)求证:∠D=∠F;
(2)用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法). -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市计划在“十周年”庆典当天开展购物抽奖活动,凡当天在该超市购物的顾客,均有一次抽奖的机会,抽奖规则如下:将如图所示的圆形转盘平均分成四个扇形,分别标上1,2,3,4四个数字,抽奖者连续转动转盘两次,当每次转盘停止后指针所指扇形内的数为每次所得的数(若指针指在分界线时重转);当两次所得数字之和为8时,返现金20元;当两次所得数字之和为7时,返现金15元;当两次所得数字之和为6时返现金10元.
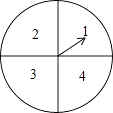
(1)试用树状图或列表的方法表示出一次抽奖所有可能出现的结果;
(2)某顾客参加一次抽奖,能获得返还现金的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
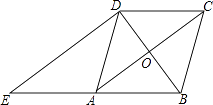
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b互为相反数,c,d互为倒数,m的绝对值是1,n是有理数且既不是正数也不是负数,求20161﹣(a+b)+m
 ﹣(cd)2016+n(a+b+c+d)的值.
﹣(cd)2016+n(a+b+c+d)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个水桶中装有少量且重量相等的水,先把甲桶的水倒出三分之一给乙桶,再把乙桶的水倒出四分之一给甲桶(假设不会溢出),最后甲、乙两桶中水的重量的大小是( )
A. 甲桶中水的重量>乙桶中水的重量 B. 甲桶中水的重量=乙桶中水的重量
C. 甲桶中水的重量<乙桶中水的重量 D. 不能确定,与桶中原有水的重量有关
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形OABC如图放置,O为原点.若点A(﹣1,2),点B的纵坐标是
 ,则点C的坐标是( )
,则点C的坐标是( )
A. (4,2) B. (2,4) C. (
 ,3) D. (3,
,3) D. (3, )
)
相关试题

