【题目】今年端午前夕,某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,对某小区居民进行了抽样调查,并将调查情况绘制成图1、图2两幅统计图(尚不完整),请根据统计图解答下列问题:

(1)参加抽样调查的居民有多少人?
(2)将两幅不完整的统计图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数.
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小韦吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
参考答案:
【答案】(1)600;(2)作图见解析;(3)3200;(4)![]() .
.
【解析】分析:(1)用B小组的频数除以B小组所占的百分比即可求得结论;
(2)分别求得C小组的频数及其所占的百分比即可补全统计图;
(3)用总人数乘以D小组的所占的百分比即可;
(4)列出树形图即可求得结论.
本题解析:(1)60÷10%=600(人).
答:本次参加抽样调查的居民有600人.
(2)如图;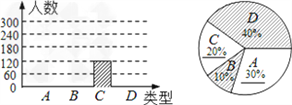
(3)7000×30%=2100(人).
(4)如图
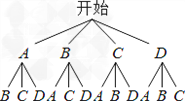
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段
 ,
,  和
和 ,求作△ABC,使
,求作△ABC,使 ,
, 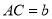 ,
,  边上的中线
边上的中线 ,作法合理的顺序依次为( )
,作法合理的顺序依次为( )①延长
 到B,使
到B,使 ;②连接
;②连接 ;③作△ADC,使
;③作△ADC,使 ,
,  ,
,  .
.A. ③①② B. ①②③ C. ②③① D. ③②①
【答案】A
【解析】试题分析:需先作△ADC,进而延长,连接即可.
根据已知条件,能够确定的三角形是△ADC,故先作△ADC,使DC=
 a,AC=b,AD=m;再延长CD到B,使BD=CD;连接AB;即可得△ABC,
a,AC=b,AD=m;再延长CD到B,使BD=CD;连接AB;即可得△ABC,则作法的合理顺序为③②①,故选A.
考点:本题考查的是基本作图
点评:解答本题的关键是熟练掌握已知三角形的两边和其中一边上的中线作三角形的做法.
【题型】单选题
【结束】
6【题目】如图是用直尺和圆规作一个角等于已知角的示意图,则说明
 的依据是( )
的依据是( ) 

A.
 B.
B. 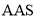 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是不等边三角形,
 ,以
,以 ,
,  为两个顶点作位置不同的三角形,使所作△DEF与△ABC全等,这样的三角形最多可以画出( )
为两个顶点作位置不同的三角形,使所作△DEF与△ABC全等,这样的三角形最多可以画出( )
A.
 个 B.
个 B.  个 C.
个 C.  个 D.
个 D.  个
个【答案】B
【解析】试题解析:如图,可以作出这样的三角形4个.

故选B.
【题型】单选题
【结束】
9【题目】作三角形用到的基本作图是:
(1)___________________________;(2)_______________________________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
 ,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.
,经过A(1,0)、B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边△ABC.(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM=
 S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长(不需要写过程).

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了推进我市校园体育运动的发展,2017年义乌市中小学运动会在雪峰中学成功举办.在此期间,某体育文化用品商店计划一次性购进篮球和排球共60个,其进价与售价间的关系如下表:
篮球
排球
进价(元/个)
80
50
售价(元/个)
105
70
(1)商店用4200元购进这批篮球和排球,求购进篮球和排球各多少个?
(2)设商店所获利润为y(单位:元),购进篮球的个数为x(单位:个),请写出y与x之间的函数关系式(不要求写出x的取值范围);
(3)若要使商店的进货成本在4300元的限额内,且全部销售完后所获利润不低于1400元,请你列举出商店所有进货方案,并求出最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
(1)起点A与终点B之间相距多远?
(2)哪支龙舟队先出发?哪支龙舟队先到达终点?
(3)分别求甲、乙两支龙舟队的y与x函数关系式;
(4)甲龙舟队出发多长时间时两支龙舟队相距200米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l的解析式为y=
 x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).
x+b,它与坐标轴分别交于A、B两点,其中B坐标为(0,4).(1)求出A点的坐标;
(2)若点 P在y轴上,且到直线l的距离为3,试求点P的坐标;
(3)在第一象限的角平分线上是否存在点Q使得∠QBA=90°?若存在,求点Q的坐标;若不存在,请说明理由.
(4)动点C从y轴上的点(0,10)出发,以每秒1cm的速度向y轴负半轴方向运动,求出点C运动中所有可能的时间t值,使得△ABC为轴对称图形.

相关试题

