【题目】下列说法:①(﹣2)101+(﹣2)100=﹣2100;②20172+2017一定可以被2018整除;③16.9×![]() +15.1×
+15.1×![]() 能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
能被4整除;④两个连续奇数的平方差是8的倍数.其中说法正确的个数是( )
A. 4个 B. 3个 C. 2个 D. 1个
参考答案:
【答案】A
【解析】
直接利提取公因式法及平方差公式法分解因式计算即可得出答案.
①(﹣2)101+(﹣2)100=(﹣2)100×(﹣2+1)=﹣2100,故此选项正确;
②20172+2017=2017×(2017+1)
=2017×2018,
故此式一定可以被2018整除,故此选项正确;
③16.9×![]() +15.1×
+15.1×![]() =
=![]() ×(16.9+15.1)=4,故此式能被4整除,故此选项正确;
×(16.9+15.1)=4,故此式能被4整除,故此选项正确;
④∵(2n+1)2﹣(2n﹣1)2
=(2n+1+2n-1)(2n+1-2n+1)
=8n,
故两个连续奇数的平方差是8的倍数,故此选项正确;
故正确的有4个.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造,供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A,B之间的距离为300(
 +1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
+1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果.

下面有三个推断:
①当投掷次数是500时,计算机记录“钉尖向上”的次数是308,所以“钉尖向上”的概率是0.616;
②随着实验次数的增加,“钉尖向上”的频率总在0.618附近摆动,显示出一定的稳定性,可以估计“钉尖向上”的概率是0.618;
③若再次用计算机模拟实验,则当投掷次数为1000时,“钉尖向上”的概率一定是0.620.
其中合理的是( )
A. ① B. ② C. ①② D. ①③
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:∠1=∠2,EG平分∠AEC.
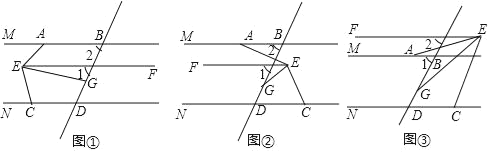
(1)如图①,∠MAE=45°,∠FEG=15°,∠NCE=75°.求证:AB∥CD;
(2)如图②,∠MAE=140°,∠FEG=30°,当∠NCE= °时,AB∥CD;
(3)如图②,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD;
(4)如图③,请你直接写出∠MAE、∠FEG、∠NCE之间满足什么关系时,AB∥CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在
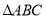 中,
中,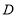 是
是 的中点,
的中点,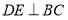 ,垂足为
,垂足为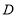 ,交
,交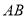 于点
于点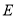 ,且
,且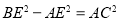 .
.(1)求
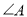 的度数;
的度数;(2)若
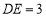 ,
,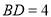 ,求
,求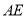 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B、C分别是线段A1B、B1C、C1A的中点,若△A1BlC1的面积是14,那么△ABC的面积是( )

A.2B.
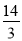 C.3D.
C.3D.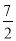
-
科目: 来源: 题型:
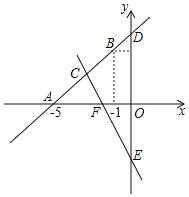
查看答案和解析>>【题目】如图,直线y=kx+b经过点A(-5,0),B(-1,4)
(1)求直线AB的表达式;
(2)求直线CE:y=-2x-4与直线AB及y轴围成图形的面积;
(3)根据图象,直接写出关于x的不等式kx+b>-2x-4的解集.
相关试题

