搜索
【题目】已知x=5是方程ax﹣8=20+a的解，则a= ．
参考答案：
【答案】7
【解析】解：把x=5代入方程ax﹣8=20+a
得：5a﹣8=20+a，
解得：a=7．
故答案为：7．
使方程左右两边相等的未知数的值是该方程的解．将方程的解代入方程可得关于a的一元一次方程，从而可求出a的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】2016年《政府工作报告》中提出了十大新词汇，为了解同学们对新词汇的关注度，某数学兴趣小组选取其中的A：“互联网+政务服务”，B：“工匠精神”，C：“光网城市”，D：“大众旅游时代”四个热词在全校学生中进行了抽样调查，要求被调查的每位同学只能从中选择一个我最关注的热词．根据调查结果，该小组绘制了如下的两幅不完整的统计图．
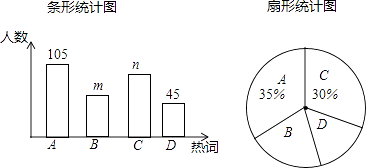
请你根据统计图提供的信息，解答下列问题：
（1）本次调查中，一共调查了多少名同学？
（2）条形统计图中，m= ， n=；
（3）扇形统计图中，热词B所在扇形的圆心角是多少度？ -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：48°29′+67°41′= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】命题“如果x2=4，那么x=2”是__________命题（填“真”或“假”）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，AB=10，AC=2
，BC边上的高AD=6，则另一边BC等于 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】请阅读下列材料：
小明遇到这样一个问题：如图1，在边长为a(a＞2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠GHN=∠DEP=45°时，求正方形MNPQ的面积．
小明发现，分别延长QE，MF，NG，PH交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形(如图2) ．
请回答：
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙不重叠)，则这个新正方形的边为 ；
(2)求正方形MNPQ的面积．
(3)参考小明思考问题的方法，解决问题：
如图3，在等边△ABC各边上分别截取AD=BE=CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ．若S△RPQ=
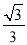，求AD的长．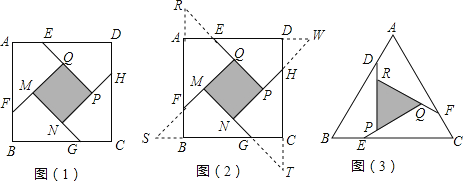 
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列分解因式正确的是( )
A. m3-m=m(m-1)(m+1) B. x2-x-6=x(x-1)-6 C. 2a2+ab+a=a(2a+b) D. x2-y2=(x-y)2
相关试题
