搜索
【题目】在△ABC中，AB=10，AC=2 
，BC边上的高AD=6，则另一边BC等于 ．
参考答案：
【答案】10或6
【解析】解：根据题意画出图形，如图所示， 如图1所示，AB=10，AC=2 
，AD=6，
在Rt△ABD和Rt△ACD中，
根据勾股定理得：BD= 
=8，CD= 
=2，
此时BC=BD+CD=8+2=10；
如图2所示，AB=10，AC=2 ，AD=6，
在Rt△ABD和Rt△ACD中，
根据勾股定理得：BD= =8，CD= =2，
此时BC=BD﹣CD=8﹣2=6，
则BC的长为6或10．
故答案为：10或6．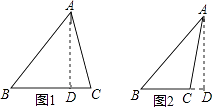
分两种情况考虑，如图所示，分别在Rt△ABC与Rt△ACD中，利用勾股定理求出BD与CD的长，即可求出BC的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：48°29′+67°41′= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】命题“如果x2=4，那么x=2”是__________命题（填“真”或“假”）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知x=5是方程ax﹣8=20+a的解，则a= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】请阅读下列材料：
小明遇到这样一个问题：如图1，在边长为a(a＞2)的正方形ABCD各边上分别截取AE=BF=CG=DH=1，当∠AFQ=∠BGM=∠GHN=∠DEP=45°时，求正方形MNPQ的面积．
小明发现，分别延长QE，MF，NG，PH交FA，GB，HC，ED的延长线于点R，S，T，W，可得△RQF，△SMG，△TNH，△WPE是四个全等的等腰直角三角形(如图2) ．
请回答：
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙不重叠)，则这个新正方形的边为 ；
(2)求正方形MNPQ的面积．
(3)参考小明思考问题的方法，解决问题：
如图3，在等边△ABC各边上分别截取AD=BE=CF，再分别过点D，E，F作BC，AC，AB的垂线，得到等边△RPQ．若S△RPQ=
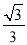，求AD的长．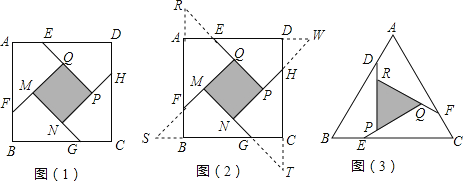 
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列分解因式正确的是( )
A. m3-m=m(m-1)(m+1) B. x2-x-6=x(x-1)-6 C. 2a2+ab+a=a(2a+b) D. x2-y2=(x-y)2
-
科目： 来源： 题型：
查看答案和解析>>【题目】多项式x2+2mx+64是完全平方式，则m=________．
相关试题
