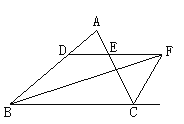
【题目】如图所示:∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E.
问:(1)图中有几个等腰三角形?为什么?
(2)BD,CE,DE之间存在着什么关系?请证明.
参考答案:
【答案】(1)图中等腰三角形有△BDF,△CEF。 2′
∵BF平分∠ABC,∴∠DBF=∠CBF,∵DF∥BC,∠FBC=∠DFB,
∴∠DBF=∠DFB,∴△DBF是等腰三角形; 4′
 6′
6′
![]() 8′
8′
【解析】(1)根据已知条件,BF、CF分别平分∠ABC、∠ACB的外角,且DE∥BC,可得∴∠DBF=∠DFB,∠ECF=∠EFC,因此可判断出△BDF和△CEF为等腰三角形;
(2)由(1)可得出DF=BD,CE=EF,所以得BD-CE=DE.
-
科目: 来源: 题型:
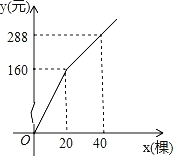
查看答案和解析>>【题目】(2016湖北省荆州市第22题)为更新果树品种,某果园计划新购进A、B两个品种的果树苗栽植培育,若计划购进这两种果树苗共45棵,其中A种苗的单价为7元/棵,购买B种苗所需费用y(元)与购买数量x(棵)之间存在如图所示的函数关系.
(1)求y与x的函数关系式;
(2)若在购买计划中,B种苗的数量不超过35棵,但不少于A种苗的数量,请设计购买方案,使总费用最低,并求出最低费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,连结CE交AD于点F,连结BD交CE于点G,连结BE.下列结论中: ①CE=BD; ②∠ADC=90°, ③
 ④
④ ,正确的是( )
,正确的是( ) 
A. ①②③④ B. ①②③ C. ①④ D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2016浙江省温州市第9题)如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片做三次折叠:第一次使点A落在C处;将纸片展平做第二次折叠,使点B落在C处;再将纸片展平做第三次折叠,使点A落在B处.这三次折叠的折痕长依次记为a,b,c,则a,b,c的大小关系是( )
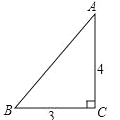
A.c>a>b B.b>a>c C.c>b>a D.b>c>a
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出命题“等腰三角形底边上的高线与顶角平分线重合”的逆命题,这个逆命题是真命题吗?请证明你的结论
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(﹣5,﹣7)关于原点对称的点的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】PM2.5是指大气中直径小于或等于2.5微米(0.0000000025米)的颗粒物,也称为可入肺颗粒物,2.5微米用科学记数法表示为米.
相关试题

