【题目】如图,在△ABC中,AB=AC,点D是BC边上的中点,DE、DF分别垂直AB、AC于点E和F.
求证:DE=DF.
参考答案:
【答案】证明:
证法一:连接AD.
∵AB=AC,点D是BC边上的中点
∴AD平分∠BAC(三线合一性质),
∵DE、DF分别垂直AB、AC于点E和F.
∴DE=DF(角平分线上的点到角两边的距离相等).
证法二:在△ABC中,
∵AB=AC
∴∠B=∠C(等边对等角)
∵点D是BC边上的中点
∴BD=DC
∵DE、DF分别垂直AB、AC于点E和F
∴∠BED=∠CFD=90°
在△BED和△CFD中
∵  ,
,
∴△BED≌△CFD(AAS),
∴DE=DF(全等三角形的对应边相等).
【解析】D是BC的中点,那么AD就是等腰三角形ABC底边上的中线,根据等腰三角形三线合一的特性,可知道AD也是∠BAC的角平分线,根据角平分线的点到角两边的距离相等,那么DE=DF.
【考点精析】掌握等腰三角形的性质是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠AOB=90°,射线OC绕点O从OA位置开始,以每秒4°的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1°的速度逆时针方向旋转.当OC与OA成180°时,OC与OD同时停止旋转.

(1)当OC旋转10秒时,∠COD= °.
(2)当旋转时间为 秒时,OC与OD的夹角是30°.
(3)当旋转时间为 秒时,OB平分∠COD时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中有五个半圆,四个小圆的直径刚好在大圆的直径上,且直径之和等于大圆直径,两只小虫同时从点A出发,以相同的速度爬向点B,甲虫沿大圆圆周运动,乙虫沿其余四个小圆的圆弧的路线爬行,则下列结论正确的是()
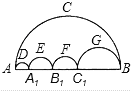
A. 甲先到点B B. 乙先到点B C. 甲、乙同时到达点B D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“菱形是对角线互相垂直的四边形”的逆命题是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个月内,小丽的体重增长﹣1千克,意思就是这个月内( )
A.小丽的体重减少﹣1千克
B.小丽的体重增长1千克
C.小丽的体重减少1千克
D.小丽的体重没变化 -
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件20元,售价为每件30元,毎个月可买出180件:如果每件商品的售价每上涨1元,则每个月就会少卖出10件,但每件售价不能高于35元,毎件商品的售价为多少元时,每个月的销售利润将达到1920元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘轮船以18海里/时的速度由西向东航行,在A处测得小岛C在北偏东75°方向上,两小时后,轮船在B处测得小岛C在北偏东60°方向上,在小岛周围15海里处有暗礁,若轮船仍然按18海里/时的速度向东航行,请问是否有触礁危险?并说明理由.

相关试题

