【题目】如图,点D、E分别在线段AB、AC上且∠ABC=∠AED , 若DE=4,AE=5,BC=8,则AB的长为( ) 
A.![]()
B.10
C.![]()
D.![]()
参考答案:
【答案】B
【解析】解答:∵∠ABC=∠AED , ∠A=∠A , ∴ADE∽△ACB ,
∴ ![]() =
= ![]() ,
,
∵DE=4,AE=5,BC=8,
∴AB=10,
故选:B .
分析:根据已知∠ABC=∠AED , ∠A=∠A , 证明△ADE∽△ACB , 根据相似三角形的性质,列出比例式,代入已知数据求出AB的长.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】要测量旗杆高CD , 在B处立标杆AB=2.5cm,人在F处.眼睛E、标杆顶A、旗杆顶C在一条直线上.已知BD=3.6m,FB=2.2m,EF=1.5m.求旗杆的高度.
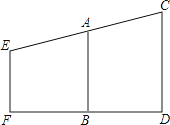
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在5×5的正方形网格中,从在格点上的点A,B,C,D中任取三点,所构成的三角形恰好是直角三角形的个数为( )

A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O , 则
 等于( )
等于( ) 
A.
B.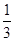
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D , E分别在AB , AC上,DE∥BC , AD=CE . 若AB:AC=3:2,BC=10,则DE的长为( )

A.3
B.4
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,O为坐标系原点,A(3,0),B(3,1),C(0,1),将△OAB沿直线OB折叠,使得点A落在点D处,OD与BC交于点E,则OD所在直线的解析式为( )
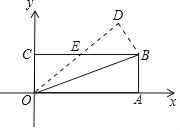
A.
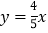 B.
B. 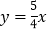 C.
C. 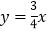 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E为CD上一点,连接AE、BD , 且AE、BD交于点F , DE:EC=2:3,则S△DEF:S△ABF=( )
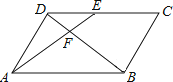
A.2:3
B.4:9
C.2:5
D.4:25
相关试题

