【题目】(知识背景)
据我国古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三、股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
(应用举例)
观察3,4,5;5,12,13;7,24,25;…
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且
勾为3时,股![]() ,弦
,弦![]() ;
;
勾为5时,股![]() ,弦
,弦![]() ;
;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24= 弦25=
(2)如果勾用![]() (
(![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股= ,弦= .
的式子表示股和弦,则股= ,弦= .
(解决问题)
观察4,3,5;6,8,10;8,15,17;…根据应用举例获得的经验进行填空:
(3)如果![]() 是符合同样规律的一组勾股数,
是符合同样规律的一组勾股数,![]() (
(![]() 表示大于1的整数),则
表示大于1的整数),则![]() ,
,![]() ,这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式.
,这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式.
(4)请你利用柏拉图公式,补全下面两组勾股数(数据从小到大排列)第一组: 、24、 :第二组: 、 、37.
参考答案:
【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() ;
;![]() ;(3)
;(3)![]() ;
;![]() ;(4)10;26; 12;35;
;(4)10;26; 12;35;
【解析】
(1)依据规律可得,如果勾为7,则股24=![]() ,
,
弦25=![]() ;
;
(2)如果勾用n(n≥3,且n为奇数)表示时,则股=![]() ,
,
弦=![]() ;
;
(3)根据规律可得,如果a,b,c是符合同样规律的一组勾股数,a=2m(m表示大于1的整数),则b=m2-1,c=m2+1;
(4)依据柏拉图公式,若m2-1=24,则m=5,2m=10,m2+1=26;若m2+1=37,则m=6,2m=12,m2-1=35.
解:(1)依据规律可得,如果勾为7,则股24=![]() ,
,
弦25=![]() ;
;
故答案为:![]() ;
;![]() ;
;
(2)如果勾用n(n≥3,且n为奇数)表示时,则股=![]() ,
,
弦=![]() ;
;
故答案为:![]() ;
;![]() ;
;
(3)根据规律可得,如果a,b,c是符合同样规律的一组勾股数,a=2m(m表示大于1的整数),则b=m2-1,c=m2+1;
故答案为:m2-1,m2+1;
(4)依据柏拉图公式,
若m2-1=24,则m=5,2m=10,m2+1=26;
若m2+1=37,则m=6,2m=12,m2-1=35;
故答案为:10、26;12、35.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(﹣1,0)、B(4,0).
(1)求此二次函数的表达式;
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(﹣
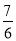 ,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;
,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;(3)如图2,点M在抛物线上,且点M的横坐标是1,将射线MA绕点M逆时针旋转45°,交抛物线于点P,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】方法感悟:
(1)如图①,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,是否在边BC、CD上分别存在点G、H,使得四边形EFGH的周长最小?若存在,求出它周长的最小值;若不存在,请说明理由.
问题解决:
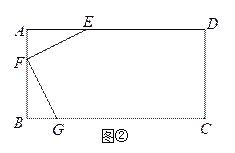
(2)如图②,有一矩形板材ABCD,AB=3米,AD=6米,现想从此板材中裁出一个面积尽可能大的四边形EFGH部件,使∠EFG=90°,EF=FG=
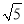 米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.
米,∠EHG=45°,经研究,只有当点E、F、G分别在边AD、AB、BC上,且AF<BF,并满足点H在矩形ABCD内部或边上时,才有可能裁出符合要求的部件,试问能否裁得符合要求的面积尽可能大的四边形EFGH部件?若能,求出裁得的四边形EFGH部件的面积,并写出在以B为坐标原点,直线BC为x轴,直线BA为y轴的坐标系中,点H的坐标;若不能,请说明理由.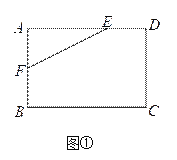
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个数值转换机,原理如图所示,若开始输入的x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,...依次继续下去
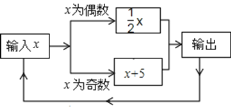
(1)请列式计算第3次到第8次的输出结果;
(2)你根据(1)中所得的结果找到了规律吗?计算2013次输出的结果是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
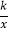 的图象与一次函数y=
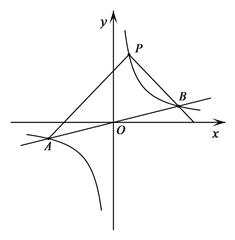
的图象与一次函数y=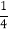 x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.
x的图象交于点A、B,点B的横坐标是4.点P是第一象限内反比例函数图象上的动点,且在直线AB的上方.(1)若点P的坐标是(1,4),直接写出k的值和△PAB的面积;
(2)设直线PA、PB与x轴分别交于点M、N,求证:△PMN是等腰三角形;
(3)设点Q是反比例函数图象上位于P、B之间的动点(与点P、B不重合),连接AQ、BQ,比较∠PAQ与∠PBQ的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数
 的图象与y轴的正半轴交于点A,其顶点B在
的图象与y轴的正半轴交于点A,其顶点B在 轴的负半轴上,且OA=OB,对于下列结论:①
轴的负半轴上,且OA=OB,对于下列结论:①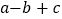 ≥0;②
≥0;② ;③关于
;③关于 的方程
的方程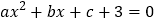 无实数根;④
无实数根;④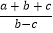 的最小值为3.其中正确结论的个数为( )
的最小值为3.其中正确结论的个数为( ) 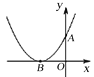
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】知识再现:
如果
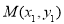 ,
,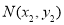 ,则线段
,则线段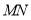 的中点坐标为
的中点坐标为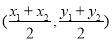 ;对于两个一次函数
;对于两个一次函数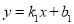 和
和 ,若两个一次函数图象平行,则
,若两个一次函数图象平行,则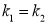 且
且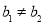 ;若两个一次函数图象垂直,则
;若两个一次函数图象垂直,则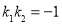 .
.提醒:在下面这个相关问题中如果需要,你可以直接利用以上知识.
在平面直角坐标系中,已知点
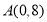 ,
,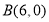 .
.(1)如图1,把直线
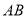 向右平移使它经过点
向右平移使它经过点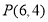 ,如果平移后的直线交
,如果平移后的直线交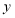 轴于点
轴于点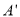 ,交x轴于点
,交x轴于点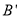 ,请确定直线
,请确定直线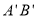 的解析式.
的解析式.(2)如图2,连接
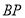 ,求
,求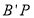 的长.
的长.(3)已知点
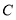 是直线
是直线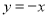 上一个动点,以
上一个动点,以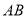 为对角线的四边形
为对角线的四边形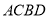 是平行四边形,当
是平行四边形,当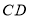 取最小值时,请在图3中画出满足条件的
取最小值时,请在图3中画出满足条件的 ,并直接写出此时
,并直接写出此时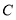 点坐标.
点坐标.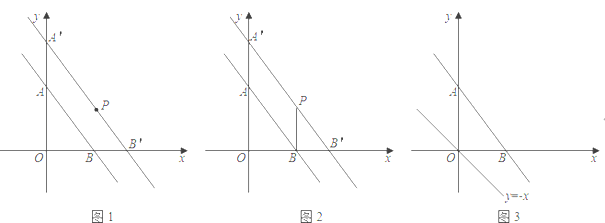
相关试题

