【题目】如图,在矩形ABCD中,AD=2AB,点E,F分别是AD,BC的中点,连接AF与BE,CE与DF分别交于点M,N两点,则四边形EMFN是( )

A. 正方形 B. 菱形 C. 矩形 D. 无法确定
参考答案:
【答案】A
【解析】∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
又∵E,F分别为AD,BC中点,
∴AE∥BF,AE=BF,ED∥CF,DE=CF,
∴四边形ABFE为平行四边形,四边形BFDE为平行四边形,
∴BE∥FD,即ME∥FN,
同理可证EN∥MF,
∴四边形EMFN为平行四边形,
∵四边形ABFE为平行四边形,∠ABC为直角,
∴ABFE为矩形,
∴AF,BE互相平分于M点,
∴ME=MF,
∴四边形EMFN为菱形。
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=1时,函数图象过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a>0,则当x≥1时,y随x的增大而减小
D.若a<0,则当x≤1时,y随x的增大而增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )

A. y=
 B. y=
B. y= C. y=
C. y= D. y=
D. y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1 , 另两张直角三角形纸片的面积都为S2 , 中间一张正方形纸片的面积为S3 , 则这个平行四边形的面积一定可以表示为( )
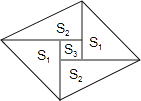
A.4S1
B.4S2
C.4S2+S3
D.3S1+4S3 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
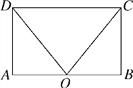
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于点H,连接OH,求证:∠DHO=∠DCO.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图案是用长度相同的火柴棒按一定规律拼搭而成,图案①需8根火柴棒,图案②需15根火柴棒,…,按此规律,图案⑦需根火柴棒.

相关试题

